views
- Decimals are a combination of whole and fractional numbers. Whole numbers go to the left of the decimal point and fractional numbers go to the right.
- Transfer your decimals to a place value chart to compare their values and order them correctly.
- Draw your decimals on a number line to see which ones are the largest and smallest.
Using a Place Value Chart
Compare the whole numbers in your list of decimals. Check out the number to the left of the decimal point—this is known as a whole number. If one decimal in the list has a higher whole number than the others, it’s automatically the greatest number. If a decimal in the list has a smaller whole number than the others on the list, it’s automatically the smallest number. Let’s say your homework asks you to order the decimals 12.45, 12.457, and 11.47. The whole number 11 is smaller than 12, so 11.47 is automatically going to be the smallest (least) number.

Set up a table for the remaining numbers. Create enough rows and columns for all of the digits and number spaces (including the decimal point). Going from left to right, label the columns as tens, ones, decimal, tenths, hundredths, and thousandths. Let’s go back to our old example. Since we already figured out that 11.47 is the smallest decimal, we’re left with 12.45 and 12.457 to sort. Draw a table with 6 columns and 2 rows to fit both numbers. If you were asked to order a list of decimals like 0.3, 0.4, 0.01, 0.02, and 0.5, your chart would need to have 5 rows and 4 columns (including one column for the decimal point).
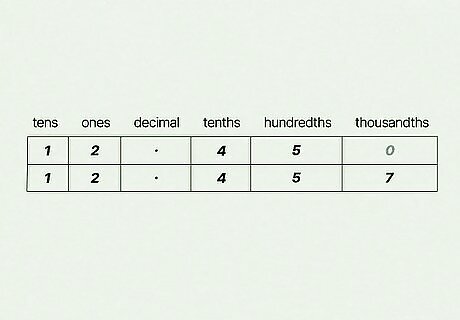
Transfer the decimals from your math problem into the table. Working from left to right, copy each decimal digit by digit into the table (don’t forget the decimal point column!). Fill in any empty portions of the table with 0 so all your decimals have the same number of digits. Let’s take a look at the two decimals in our table. The number 12.45 only has 4 digits, so you’d add a 0 to the thousandths place (making it 12.450). This makes it a lot easier to compare with 12.457, right?
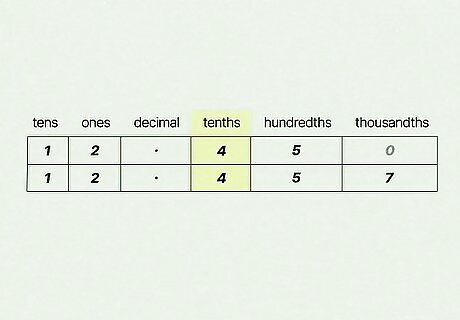
Compare the digits in the tenths column of the table. Take a peek at the tenths column—it’s immediately right of the decimal point column. Whichever decimal has a larger digit in the tenths column is automatically the larger number. If the numbers in the tenths column are identical, move on to the hundredths column instead. In our chart, both 12.45 and 12.457 have a 4 in the tenths column. So, we’d move onto the hundredths column and make a new comparison. Let’s say you’re asked to compare 0.1 and 0.01. The decimal 0.1 has a 1 in the tenths column while 0.01 only has a 0. Therefore, 0.1 is the bigger number.
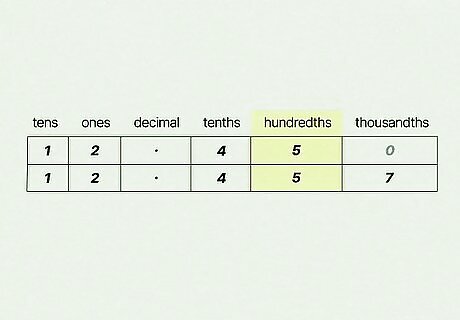
Compare the hundredths column (2 to the right of the decimal point). Is one number larger than the other, or are they both the same value? The number that has a larger digit in the hundredths column is the larger decimal overall. If both numbers are the same, move on to the thousandths column. Let’s take another glance at our table—both 12.45 and 12.457 have a 5 in the hundredths place, so you’d shift over to the thousandths column for another comparison. Pretend you were asked to compare the decimals 4.04 and 4.02. The number 4.04 has a 4 in the hundredths place while 4.02 only has a 2, which makes 4.04 the bigger decimal.

Examine the digits in the thousandths column. Move on to the next column over, which is 3 spaces to the right of your decimal point column. Take a look at this column and see which digit is bigger—this decimal is the larger number. Let’s take a final look at our table. The decimal 12.45 has a 0 in the thousandths place while 12.457 has a 7. With this in mind, 12.457 is a bigger decimal than 12.45.
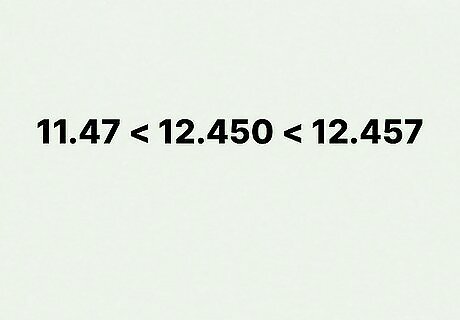
Order the numbers from least to greatest. Jot down the smallest number first—in our example, that’s 11.47. Then, write out the next largest number, followed by the largest number. In our math problem, the final answer would be: 11.47, 12.45, and 12.457.
Drawing a Number Line

Write the decimals in a vertical list. Chances are, your assignment sheet listed the decimals horizontally, which makes them pretty tough to visualize. Grab a fresh sheet of paper (or use the margins of your homework sheet) to jot down the numbers in a vertical list instead. If your assignment asks you to order the decimals 14.36, 13.458, and 14.369, you could write them like: 14.3613.45814.369

Compare the whole numbers before drawing out your number line. Examine the numbers to the left of the decimal point—these are “whole” numbers, and they’re the quickest way to compare and order your decimals right off the bat. If one whole number is bigger than the others, move it to the right side of the number line; if it’s smaller than the others, move it to the left. In our example, the number 13 is smaller than 14, so you’d automatically mark 13.458 as the smallest number.

Identify the first place value where the digits differ. Move from left to right and compare the digits in each place value. Examine each column until you find where the numbers don’t match up. Think of it like a game of spot the difference! Take 14.36 and 14.369, for instance—both decimals have a 3 in the tenths place and a 6 in the hundredths place. In the thousandths place, however, 14.36 has a 0 while 14.369 has a 9.

Set two different decimals as the lowest and highest points on your number line. Mark down the smallest decimal (in our case, 14.36) as the smallest number on the left side of your number line. Then, take the highest decimal (in our case, 14.369) and round it up to the nearest place value (making it 14.37). This rounded-up number acts as the highest decimal of your number line and goes on the far right side of the line.

Draw out your number line and divide it into tenths. Mark 10 notches that evenly separate your 2 decimals, which help you place your numbers more accurately on the number line. Then, label the notches with their corresponding decimal. In our example, the 10 notches represent 14.361, 14.362, 14.363, 14.364, 14.365, 14.366, 14.367, 14.368, 14.369, and 14.37.
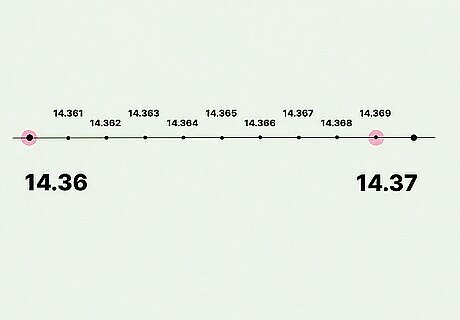
Plot the numbers you are comparing on the number line. Draw a big, obvious dot that represents each of the decimals from your list. In our example, you’d draw a dot on the first number of the number line to represent 14.36. Then, you’d draw a dot on the second-to-last number to represent 14.369.
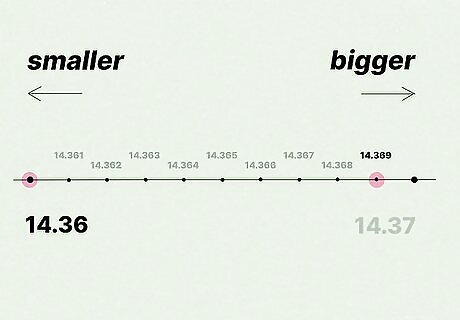
Compare the location of each number on the number line. On a number line, numbers get bigger as you go from left to right. So, the biggest number falls the furthest right on the number line, while the smallest number falls the furthest left. In our example, 14.369 falls to the right of 14.36— that makes 14.369 the larger number.

Rewrite the numbers in order from least to greatest. Jot down the smallest number first and the largest number last. Then, list any other numbers between these 2 digits, keeping them in ascending (lowest to highest) order. For our example problem, the final list would be: 13.458, 14.36, 14.369. You can also use the less than sign to show their relationship: 13.458 < 14.36 < 14,369.
Reviewing Place Values

A decimal point looks like a dot or period. It separates a number into its whole and fractional parts—the numbers to the left are whole numbers, while the numbers to the right are fractional. The numbers get bigger as you go to the left of the decimal point and get smaller as you go to the right. Let’s take a look at the decimal 12.38. For this number, the digits 1 and 2 are whole numbers, while 3 and 8 are fractional numbers. In Europe, people use a decimal comma instead of a decimal point.

The place values for whole numbers go to the left of a decimal point. A whole number is a digit that has smaller parts attached—so, numbers like 13 and 270 are whole numbers, while 13.5 or 270.2 are not. From right to left, the place values of whole numbers are ones, tens, hundreds, thousands, ten-thousands, hundred-thousands, and millions. In the number 51 the 5 digit is in the tens place. It has a value of 5 tens. In the number 50,001, the digit 5 is in the ten-thousands place—this gives it a value 5 ten-thousands, or 50,000. The smallest place value for whole numbers is the ones place. Ten sets of 1 move the 1 into the tens place, while 10 sets of 10 move the number into the hundreds place. See the pattern? This pattern continues for the higher place values.
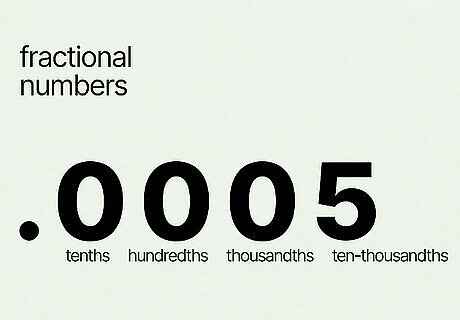
The place values for fractional numbers go to the right of the decimal point. Unlike whole numbers, fractional place values are ordered from left to right. Starting at the decimal point, the place values are tenths, hundredths, thousandths, ten-thousandths, hundred-thousandths, and millionths. For example, in the number 1.5, the digit 5 is in the tenths place. It has the value of 5 tenths, or 5 10 {\displaystyle {\frac {5}{10}}} {\frac {5}{10}}. In the number 1.0005, however, the digit 5 has a value of 5 ten-thousandths, or 5 10 , 000 {\displaystyle {\frac {5}{10,000}}} {\frac {5}{10,000}}. The tenths place is the largest place value for fractional numbers. Ten hundredths make one-tenth, 10 thousandths make 1 hundredth, and 10 ten-thousandths create 1 thousandth. When comparing fractional numbers, it helps to convert decimals into fractions: 1 10 > 1 100 {\displaystyle {\frac {1}{10}}>{\frac {1}{100}}} {\frac {1}{10}}>{\frac {1}{100}}. To convert a fraction into a decimal, simply divide the numerator by the denominator.

















Comments
0 comment