
views
X
Research source
It is easy to determine how many divisors a small integer (such as 6) has by simply listing out all the different ways you can multiply two numbers together to get to that integer. When working with larger integers, finding the number of divisors is more difficult. However, once you have factored the integer into prime factors, you can use a simple formula to reach your answer.
Factoring the Integer

Write the integer at the top of the page. You need to leave enough room so that you can set up a factor tree below it. You can use other methods to factor a number. Read Factor a Number for more instructions. For example, if you want to know many divisors, or factors, the number 24 has, write 24 {\displaystyle 24} 24 at the top of the page.

Find two numbers you can multiply together to get the number, not including 1. These are two divisors, or factors, of the number. Draw a split branch coming down from the original number, and write the two factors below it. For example, 12 and 2 are factors of 24, so draw a split branch coming down from 24 {\displaystyle 24} 24, and write the numbers 12 {\displaystyle 12} 12 and 2 {\displaystyle 2} 2 below it.

Look for prime factors. A prime factor is a number that is only evenly divisible by 1 and itself. For example, 7 is a prime number, because the only numbers that evenly divide into 7 are 1 and 7. Circle any prime factors so that you can keep track of them. For example, 2 is a prime number, so you would circle the 2 {\displaystyle 2} 2 on your factor tree.
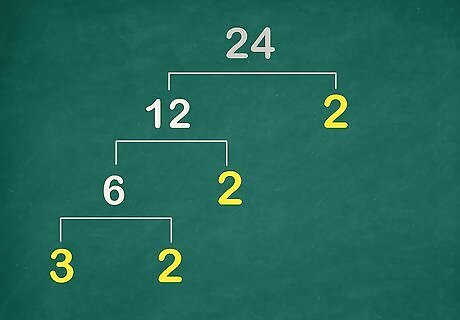
Continue to factor non-prime numbers. Keep drawing branches down from the non-prime factors until all of your factors are prime. Circle the prime numbers to keep track of them. For example, 12 can be factored into 6 {\displaystyle 6} 6 and 2 {\displaystyle 2} 2. Since 2 {\displaystyle 2} 2 is a prime number, you would circle it. Next, 6 {\displaystyle 6} 6 can be factored into 3 {\displaystyle 3} 3 and 2 {\displaystyle 2} 2. Since 3 {\displaystyle 3} 3 and 2 {\displaystyle 2} 2 are prime numbers, you would circle them.
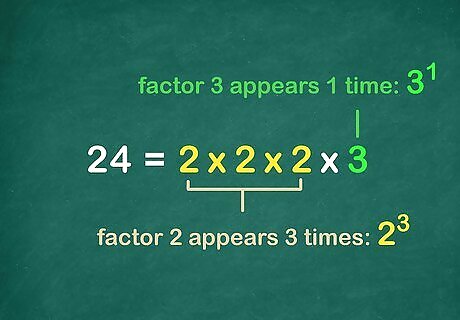
Write an exponential expression for each prime factor. To do this, look for multiples of each prime factor in your factor tree. The number of times the factor appears equals the exponent of the factor in your exponential expression. For example, the prime factor 2 {\displaystyle 2} 2 appears three times in your factor tree, so the exponential expression is 2 3 {\displaystyle 2^{3}} 2^{{3}}. The prime factor 3 {\displaystyle 3} 3 appears 1 time in your factor tree, so the exponential expression is 3 1 {\displaystyle 3^{1}} 3^{{1}}.
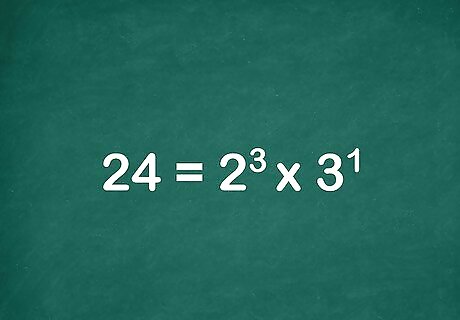
Write the equation for the prime factorization of the number. The original number you are working with is equal to the product of the exponential expressions. For example 24 = 2 3 × 3 1 {\displaystyle 24=2^{3}\times 3^{1}} 24=2^{{3}}\times 3^{{1}}.
Determining the Number of Factors
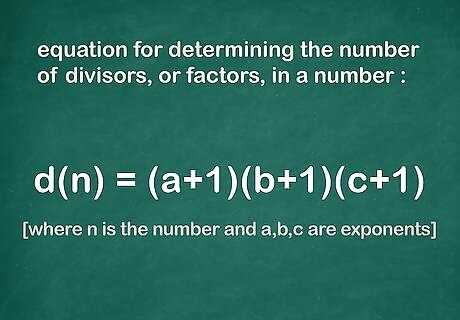
Set up the equation for determining the number of divisors, or factors, in a number. The equation is d ( n ) = ( a + 1 ) ( b + 1 ) ( c + 1 ) {\displaystyle d(n)=(a+1)(b+1)(c+1)} d(n)=(a+1)(b+1)(c+1), where d ( n ) {\displaystyle d(n)} d(n) is equal to the number of divisors in the number n {\displaystyle n} n, and a {\displaystyle a} a, b {\displaystyle b} b, and c {\displaystyle c} c are the exponents in the prime factorization equation for the number. You might have less than three or more than three exponents. The formula simply states to multiply together whatever number of exponents you are working with.
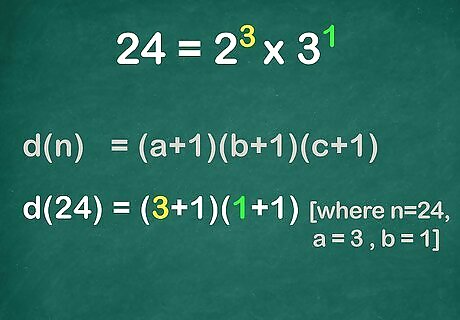
Plug in the value of each exponent into the formula. Be careful to use the exponents, not the prime factors. For example, since 24 = 2 3 × 3 1 {\displaystyle 24=2^{3}\times 3^{1}} 24=2^{{3}}\times 3^{{1}}, you would plug in the exponents 3 {\displaystyle 3} 3 and 1 {\displaystyle 1} 1 into the equation. Thus the equation will look like this: d ( 24 ) = ( 3 + 1 ) ( 1 + 1 ) {\displaystyle d(24)=(3+1)(1+1)} d(24)=(3+1)(1+1).
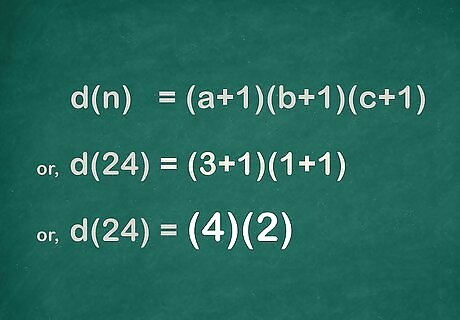
Add the values in parentheses. You are simply adding 1 to each exponent. For example: d ( 24 ) = ( 3 + 1 ) ( 1 + 1 ) {\displaystyle d(24)=(3+1)(1+1)} d(24)=(3+1)(1+1) d ( 24 ) = ( 4 ) ( 2 ) {\displaystyle d(24)=(4)(2)} d(24)=(4)(2)
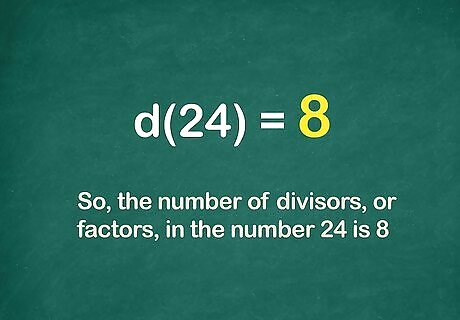
Multiply the values in parentheses. The product will equal the number of divisors, or factors, in the number n {\displaystyle n} n. For example: d ( 24 ) = ( 4 ) ( 2 ) {\displaystyle d(24)=(4)(2)} d(24)=(4)(2) d ( 24 ) = 8 {\displaystyle d(24)=8} d(24)=8So, the number of divisors, or factors, in the number 24 is 8.



















Comments
0 comment