
views
Calculating the Range

Determine the highest measured value. It helps to begin by sorting your data in numerical order, from lowest to highest. This will ensure that you do not miss any values. Then select the value at the end of the list. For example, suppose you are testing the precision of a scale, and you observe five measurements: 11, 13, 12, 14, 12. After sorting, these values are listed as 11, 12, 12, 13, 14. The highest measurement is 14.

Find the lowest measured value. Once your data has been sorted, finding the lowest value is as simple as looking at the beginning of the list. For the scale measurement data, the lowest value is 11.
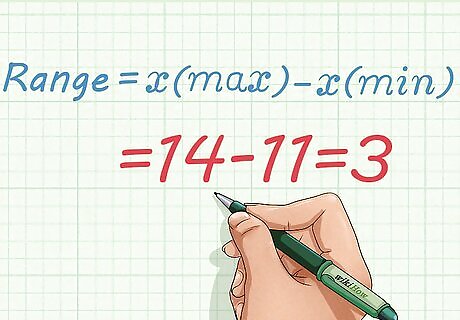
Subtract the lowest value from the highest. The range of a set of data is the difference between the highest and lowest measurements. Just subtract one from the other. Algebraically, the range can be expressed as: Range = x ( m a x ) − x ( m i n ) {\displaystyle {\text{Range}}=x(max)-x(min)} {\text{Range}}=x(max)-x(min) For the sample data, the range is: Range = x ( m a x ) − x ( m i n ) = 14 − 11 = 3 {\displaystyle {\text{Range}}=x(max)-x(min)=14-11=3} {\text{Range}}=x(max)-x(min)=14-11=3
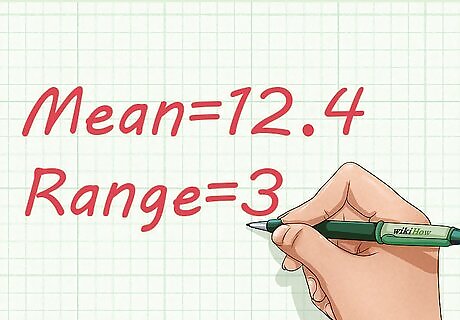
Report the range as the precision. When reporting data, it is important to let the readers know what you have measured. Because there are different measures of precision, you should specify what you are reporting. For this data, you would report Mean=12.4, Range=3, or simply that the Mean=12.4±3. The mean is not actually part of calculating the range or precision, but it is generally the primary calculation for reporting the measured value. The mean is found by adding up the sum of the measured values and then dividing by the number of items in the group. For this set of data, the mean is (11+13+12+14+12)/5=12.4.
Calculating the Average Deviation

Find the mean of the data. The average deviation is a more detailed measure of the precision of a group of measurements or experiment values. The first step in finding the average deviation is to calculate the mean of the measured values. The mean is the sum of the values, divided by the number of measurements taken. For this example, use the same sample data as before. Assume that five measurements have been taken, 11, 13, 12, 14, and 12. The mean of these values is (11+13+12+14+12)/5=12.4.

Calculate the absolute deviation of each value from the mean. For this calculation of precision, you need to determine how close each value is to the mean. To do this, subtract the mean from each number. For this measurement, it does not matter whether the value is above or below the mean. Subtract the numbers and just use the positive value of the result. This is also called the absolute value. Algebraically, the absolute value is shown by placing two vertical bars around the calculation, as follows: Absolute deviation = | x − μ | {\displaystyle {\text{Absolute deviation}}=|x-\mu |} {\text{Absolute deviation}}=|x-\mu | For this calculation, x {\displaystyle x} x represents each of the experimental values, and μ {\displaystyle \mu } \mu is the calculated mean. For the values of this sample data set, the absolute deviations are: | 12 − 12.4 | = 0.4 {\displaystyle |12-12.4|=0.4} |12-12.4|=0.4 | 11 − 12.4 | = 1.4 {\displaystyle |11-12.4|=1.4} |11-12.4|=1.4 | 14 − 12.4 | = 1.6 {\displaystyle |14-12.4|=1.6} |14-12.4|=1.6 | 13 − 12.4 | = 0.6 {\displaystyle |13-12.4|=0.6} |13-12.4|=0.6 | 12 − 12.4 | = 0.4 {\displaystyle |12-12.4|=0.4} |12-12.4|=0.4

Find the average deviation. Use the absolute deviations and find their mean. As you did with the original data set, you will add them together and divide by the number of values. This is represented algebraically as: Average deviation = Σ | x − μ | n {\displaystyle {\text{Average deviation}}={\frac {\Sigma |x-\mu |}{n}}} {\text{Average deviation}}={\frac {\Sigma |x-\mu |}{n}} For this sample data, the calculation is: Average deviation = 0.4 + 1.4 + 1.6 + 0.6 + 0.4 5 {\displaystyle {\text{Average deviation}}={\frac {0.4+1.4+1.6+0.6+0.4}{5}}} {\text{Average deviation}}={\frac {0.4+1.4+1.6+0.6+0.4}{5}} Average deviation = 4.4 5 {\displaystyle {\text{Average deviation}}={\frac {4.4}{5}}} {\text{Average deviation}}={\frac {4.4}{5}} Average deviation = 0.88 {\displaystyle {\text{Average deviation}}=0.88} {\text{Average deviation}}=0.88

Report the precision result. This result may be reported as the mean, plus or minus the average deviation. For this sample data set, this result would look like 12.4±0.88. Note that reporting precision as the average deviation makes the measurement appear much more precise than with the range.
Calculating Standard Deviation

Use the correct formula for standard deviation. For any size data set, the standard deviation is a reliable statistic for reporting precision. There are two formulas for calculating standard deviation, with a very slight difference between them. You will use one formula if your measured data represents an entire population. You will use the second formula if your measured data is from only a sample of the population. Your data represents an entire population if you have collected all the measurements possible from all possible subjects. For example, if you are conducting tests on people with some very rare disease, and you believe that you have tested everyone with that disease, then you have the entire population. The standard deviation formula in this case is: σ = Σ ( x − μ ) 2 n {\displaystyle \sigma ={\sqrt {\frac {\Sigma (x-\mu )^{2}}{n}}}} \sigma ={\sqrt {{\frac {\Sigma (x-\mu )^{2}}{n}}}} A sample set is any group of data less than an entire population. This is actually going to be used more often. The standard deviation formula for a sample set is: σ = Σ ( x − μ ) 2 n − 1 {\displaystyle \sigma ={\sqrt {\frac {\Sigma (x-\mu )^{2}}{n-1}}}} \sigma ={\sqrt {{\frac {\Sigma (x-\mu )^{2}}{n-1}}}} Notice that the only difference is in the denominator of the fraction. For an entire population, you will divide by n {\displaystyle n} n. For a sample set, you will divide by n − 1 {\displaystyle n-1} n-1.

Find the mean of the data values. As with calculating the average deviation, you will begin by finding the mean of the data values. Using the same set of measurements as above, the mean is 12.4.
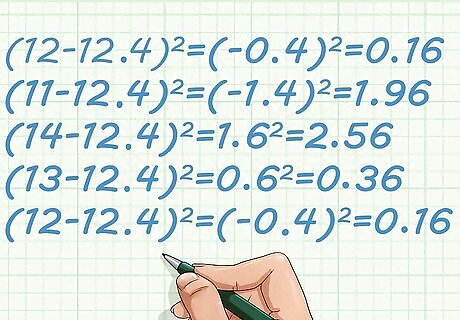
Find the square of each variation. For each data point, subtract the data value from the mean, and square that result. Because you are squaring these variations, whether the difference is positive or negative does not matter. The square of the difference will always be positive. For the five data values in this sample, these calculations are as follows: ( 12 − 12.4 ) 2 = ( − 0.4 ) 2 = 0.16 {\displaystyle (12-12.4)^{2}=(-0.4)^{2}=0.16} (12-12.4)^{2}=(-0.4)^{2}=0.16 ( 11 − 12.4 ) 2 = ( − 1.4 ) 2 = 1.96 {\displaystyle (11-12.4)^{2}=(-1.4)^{2}=1.96} (11-12.4)^{2}=(-1.4)^{2}=1.96 ( 14 − 12.4 ) 2 = 1.6 2 = 2.56 {\displaystyle (14-12.4)^{2}=1.6^{2}=2.56} (14-12.4)^{2}=1.6^{2}=2.56 ( 13 − 12.4 ) 2 = 0.6 2 = 0.36 {\displaystyle (13-12.4)^{2}=0.6^{2}=0.36} (13-12.4)^{2}=0.6^{2}=0.36 ( 12 − 12.4 ) 2 = ( − 0.4 ) 2 = 0.16 {\displaystyle (12-12.4)^{2}=(-0.4)^{2}=0.16} (12-12.4)^{2}=(-0.4)^{2}=0.16

Calculate the sum of the squared differences. The numerator of the standard deviation fraction is the sum of the squared differences between each value and the mean. To find this sum, add together the figures from the previous calculation. For the sample data set, these are: 0.16 + 1.96 + 2.56 + 0.36 + 0.16 = 5.2 {\displaystyle 0.16+1.96+2.56+0.36+0.16=5.2} 0.16+1.96+2.56+0.36+0.16=5.2

Divide by the data size. This is the one step that will differ for either a population calculation or a sample set calculation. For a full population, you will divide by n {\displaystyle n} n, the number of values. For a sample set, you will divide by n − 1 {\displaystyle n-1} n-1. This example has only five measurements and is therefore only a sample set. Thus, for the five values being used, divide by (5-1) or 4. The result is 5.2 / 4 = 1.3 {\displaystyle 5.2/4=1.3} 5.2/4=1.3.
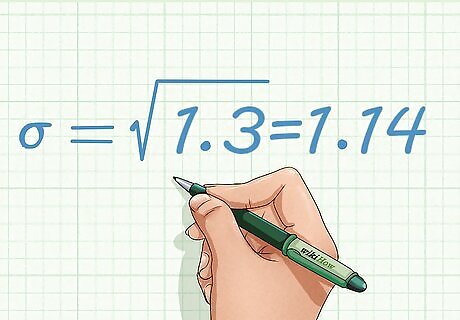
Find the square root of the result. At this point, the calculation represents what is called the variance of the data set. The standard deviation is the square root of the variance. Use a calculator to find the square root, and the result is the standard deviation. σ = 1.3 = 1.14 {\displaystyle \sigma ={\sqrt {1.3}}=1.14} \sigma ={\sqrt {1.3}}=1.14

Report your result. Using this calculation, the precision of the scale can be represented by giving the mean, plus or minus the standard deviation. For this data, this will be 12.4±1.14. The standard deviation is perhaps the most common measurement of precision. Nevertheless, for clarity, it is still a good idea to use a footnote or parentheses to note that the precision value represents the standard deviation.
Deciding How to Report Precision

Use the word precision correctly. Precision is a term that describes the level of repeatability of measurements. When collecting a group of data, either by measurement or through an experiment of some kind, the precision describes how close together the results of each measurement or experiment are going to be. Precision is not the same as accuracy. Accuracy measures how close experimental values come to the true or theoretical value, while precision measures how close the measured values are to each other. It is possible for data to be accurate but not precise or to be precise but not accurate. Accurate measurements are close to the target value but may not be close to each other. Precise measurements are close to each other, whether or not they are close to the target.

Choose the best measure of precision. The word “precision” does not have a single meaning. You can represent precision using several different measurements. You need to decide the best one. Range. For small data sets with about ten or fewer measurements, the range of values is a good measure of precision. This is particularly true if the values appear reasonably closely grouped. If you see one or two values that appear far from the others, you may wish to use a different calculation. Average deviation. The average deviation is a more accurate measure of precision for a small set of data values. Standard deviation. The standard deviation is perhaps the most recognized measure of precision. Standard deviation may be used to calculate the precision of measurements for an entire population or a sample of the population.

Report your results clearly. Very often, investigators will report data by giving the mean of the measured value, followed by a statement of the precision. The precision is shown with a “±” symbol. This provides an indication of precision, but it does not clearly explain to the reader if the number following the “±” symbol is a range, standard deviation, or some other measurement. To be very clear, you should define what measure of precision you are using, either in a footnote or parenthetical note. For example, for one series of data, the result could be reported as 12.4±3. However, a more explanatory way to report the same data would be to say “Mean=12.4, Range=3.”



















Comments
0 comment