How to Add Binary Numbers

Understanding the Binary System

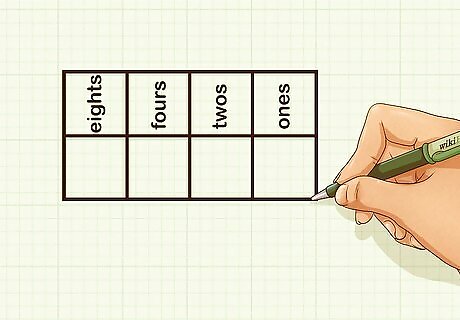
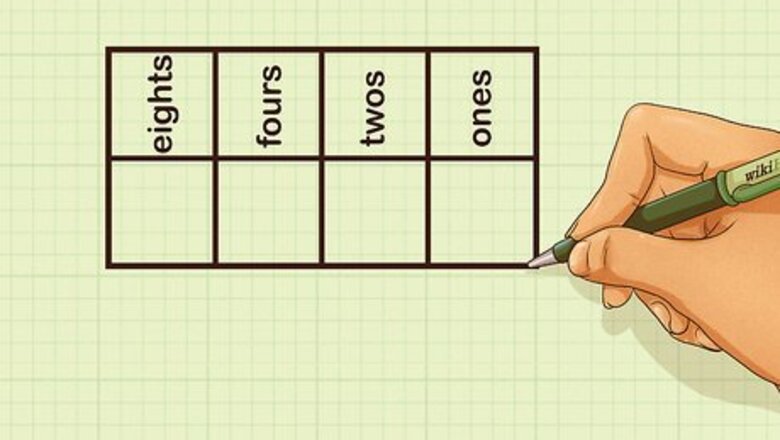
Draw a place value chart with two rows and four columns. Label each column with a place value. The binary system is a base 2 system, so instead of the ones, tens, hundreds, and thousands place like we use in the decimal (base 10) system, binary has the ones, twos, fours, and eights place. The ones place is the far right column of your chart, and the eights place is the far left column. You can continue your place value chart. Each place value is determined by a base 2 exponent. For example: 2 0 = ones place {\displaystyle 2^{0}={\text{ones place}}} 2^{{0}}={\text{ones place}} 2 1 = twos place {\displaystyle 2^{1}={\text{twos place}}} 2^{{1}}={\text{twos place}} 2 2 = fours place {\displaystyle 2^{2}={\text{fours place}}} 2^{{2}}={\text{fours place}} 2 3 = eights place {\displaystyle 2^{3}={\text{eights place}}} 2^{{3}}={\text{eights place}} 2 4 = sixteens place {\displaystyle 2^{4}={\text{sixteens place}}} 2^{{4}}={\text{sixteens place}} 2 5 = thirty-twos place {\displaystyle 2^{5}={\text{thirty-twos place}}} 2^{{5}}={\text{thirty-twos place}}

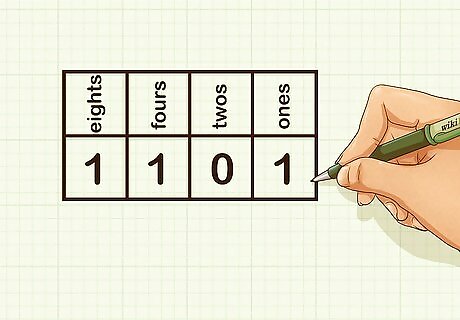
Write a random binary number in the bottom row of your chart. In the binary system, the only digits used are 1 {\displaystyle 1} 1 and 0 {\displaystyle 0} {\displaystyle 0}. For example, you might write 1 in the eights place, 1 in the fours place, 0 in the twos place, and 1 in the ones place: 1101.

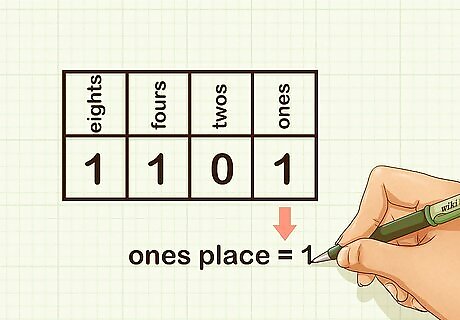
Interpret the ones place. If there is a 0 in the ones place, the value is 0. If there is a 1 in the ones place, the value is 1. For example, in the binary number 1101, there is a 1 in the ones place, so the value is 1. So the binary number 1 is equal to the decimal number 1.

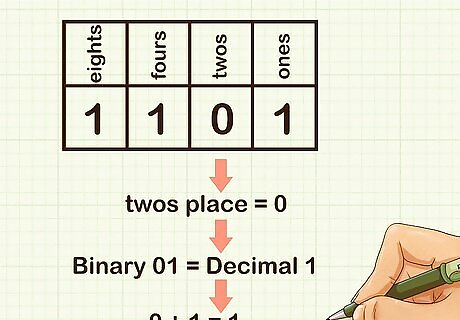
Interpret the twos place. If there is a 0 in the twos place, the value is 0. If there is a 1 in the twos place, the value is 2. For example, in the binary number 1101, there is a 0 in the twos place, so the value is 0. So the binary number 01 is equal to the decimal number 1, because there are 0 twos and 1 one: 0 + 1 = 1.

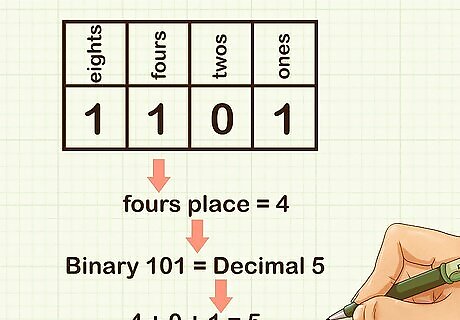
Interpret the fours place. If there is a 0 in the fours place, the value is 0. If there is a 1 in the fours place, the value is 4. For example, in the binary number 1101, there is a 1 in the fours place, so the value is 4. So the binary number 101 is equal to the decimal number 5, because there are 1 four, 0 twos, and 1 one: 4 + 0 + 1 = 5.

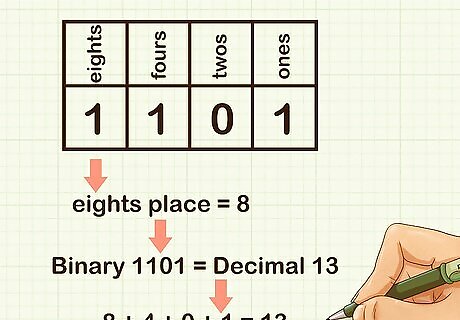
Interpret the eights place. If there is a 0 in the eights place, the value is 0. If there is a 1 in the eights place, the value is 8. For example, in the binary number 1101, there is a 1 in the eights place, so the value is 8. So the binary number 1101 is equal to the decimal number 13, because there are 1 eight, 1 four, 0 twos, and 1 one: 8 + 4 + 0 + 1 = 13.

Adding Binary Numbers Using Place Value

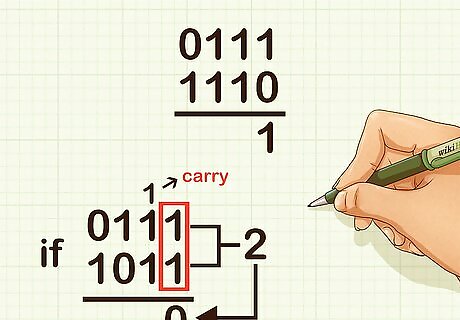
Set up the problem vertically, and add the digits in the ones place. Since you are only adding two digits, the possible sum is either 0, 1, or 2. If the sum is 0, write a 0 in the answer’s ones place. If the sum is 1, write a 1 in the answer’s ones place. If the sum is 2, write a 0 in the answer’s ones place, and carry a 1 into the twos column. For example, if adding 0111 and 1110, for the ones column you would add 1 one plus 0 ones = 1, so place a 1 in the answer’s ones column.

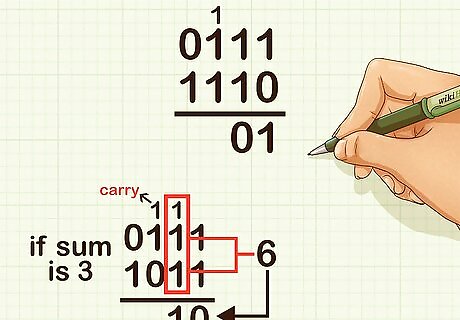
Add the digits in the twos place. The possible sum is either 0, 1, 2, or 3 (if you carried from the ones place). If the sum is 0, write a 0 in the answer’s twos place. If the sum is 1, write a 1 in the answer’s twos place. If the sum is 2, write a 0 in the answer’s twos place, and carry a 1 into the fours column. If the sum is 3, write a 1 in the answer’s twos place, and carry a 1 into the fours column (3 twos = 6 = 1 two and 1 four). For example, if adding 0111 and 1110, for the twos column you would add 1 two, plus 1 two = 2 twos = 4, so place a 0 in the answer’s twos column and carry a 1 into the fours column.

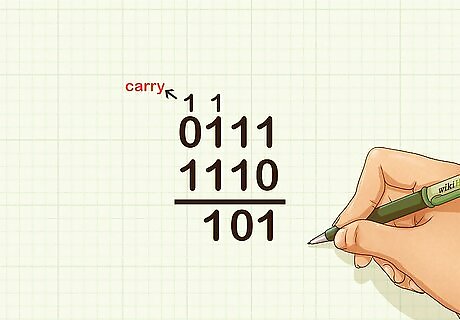
Add the digits in the fours place. The possible sum is either 0, 1, 2, or 3 (if you carried from the twos place). If the sum is 0, write a 0 in the answer’s fours place. If the sum is 1, write a 1 in the answer’s fours place. If the sum is 2, write a 0 in the answer’s fours place, and carry a 1 into the eights column. If the sum is 3, write a 1 on the answer’s fours place, and carry a 1 into the eights column (3 fours = 12 = 1 four and 1 eight). For example, if adding 0111 and 1110, for the fours column you would add 1 four, plus 1 four, plus 1 four = 3 fours= 12, so place a 1 in the answer’s fours column and carry a 1 into the eights column.

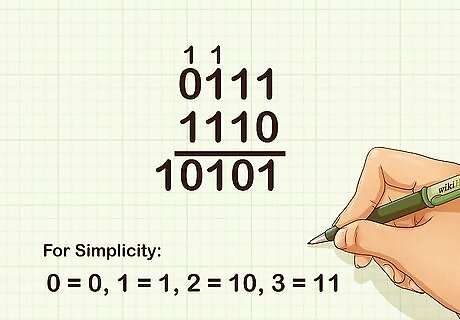
Keep adding the digits in each place value of the number until you reach your final answer. For simplicity’s sake, you can remember that 0 = 0, 1 = 1, 2 = 10, and 3 = 11. For example, if adding 0111 and 1110, for the eights column you would add up 2 eights, since you carried from the fours column. For a sum of 2, place a 0 in the eights column and carry a 1 into the sixteens column. Since there are no other numbers in the sixteens column, just bring that 1 down to the final answer. So 0111 + 1110 = 10101.

Adding Multiple Binary Numbers by Pairing 1s

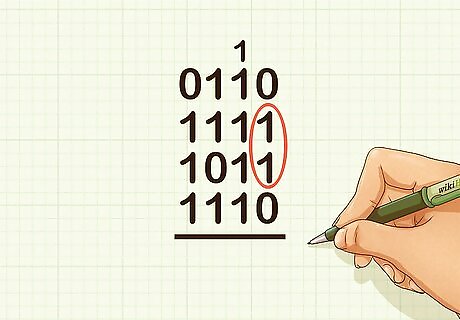
Set up the problem vertically. Circle pairs of 1s (digits) in the ones column. Remember, the ones column in binary is the far right column. For example, if adding 1010 + 1111 + 1011 + 1110, you should circle 1 pair of 1s.

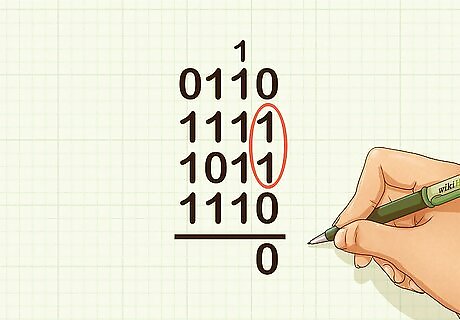
Interpret the ones column. For each pair of 1s, carry a 1 into the twos column. If there is only one 1, or if there is one 1 left over after circling pairs of 1s, then write a 1 in the answer’s ones place. If there are no 1s left over, place a 0 in the answer’s ones place. For example, since you circled one pair of 1s, you would carry a 1 into the twos column, and drop a 0 in the answer’s ones place.

Circle pairs of 1s in the twos column. Don’t forget to include any digits you carried over from the ones column. For example, if adding 1010 + 1111 + 1011 + 1110, you should circle 2 pairs of 1s, and have one 1 left over.

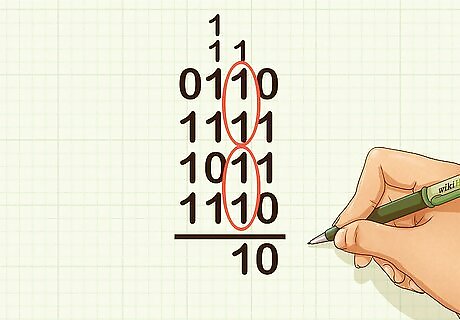
Interpret the twos column. For each pair of 1s, carry a 1 into the fours column and drop a 0 into the answer’s twos place. If there is only one 1, or if there is a 1 left over after circling pairs of 1s, then place a 1 into the answer’s twos place. If there are no 1s left over, place a 0 in the answer’s ones place. For example, since you circled 2 pairs of 1s and had one 1 leftover, you would carry a 1 into the fours column twice, and drop a 1 in the answer’s twos place.

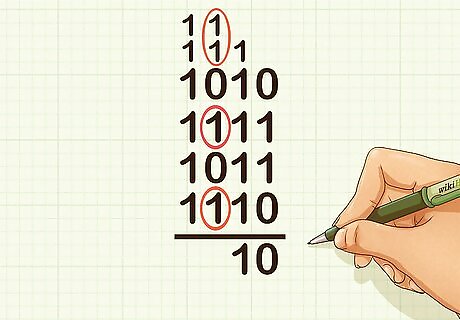
Circle pairs of 1s in the fours column. Don’t forget to include any digits you carried over from the twos column. For example, if adding 1010 + 1111 + 1011 + 1110, you should circle 2 pairs of 1s, since you carried 1 over twice from the twos column.

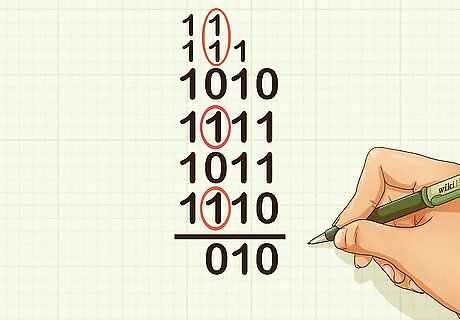
Interpret the fours column. Carry over a 1 into the eights column for each pair of 1s. Don’t forget to put a 1 in the fours place if you have one 1 left over, or a 0 in the fours place if you have no 1s left over. For example, since you circled 2 pairs of 1s with none left over, you would carry a 1 into the eights column twice, and place a 0 in the answer’s fours column.

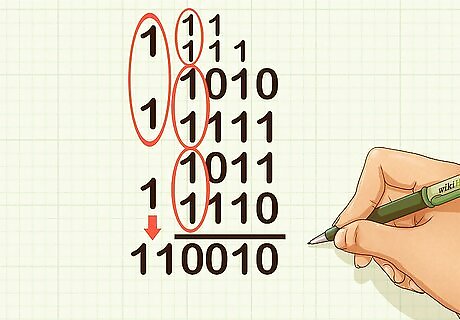
Continue circling pairs of 1s for each place value. Don’t forget to carry a 1 into the next column for each circled pair, to place a 1 in the answer if there is a 1 left over, and to place a 0 in the answer if only zeros remain in the column. For example, if adding 1010 + 1111 + 1011 + 1110, for the eights place you should circle 3 pairs of 1s, since you carried 1 over twice from the fours column. So you would place a 0 in the eights place of your answer and carry three 1s into the sixteens column. In the sixteens column you have one pair of 1s with one 1 left over, so you would place a 1 in the sixteens place of your answer, and a 1 in the thirty-twos column of your answer. So 1010 + 1111 + 1011 + 1110 = 110010.

Check your answer. There are a number of binary calculators online that will calculate the sum of binary numbers.

Adding Binary Numbers Using Boolean Operations

Perform an XOR operation in the first column to determine the result. An XOR statement will return true or 1 if the two inputs are different (such as 0 and 1) and false or 0 if the two inputs are the same.

Perform an AND operation in the first column to determine the carry to the next column. An AND operation will return true or 1 if both of the inputs are 1 and false otherwise.

Perform a repeated XOR with the carry to determine the result for the second column. The first XOR between the two inputs will determine the intermediate output to the XOR with the carry. The second XOR between the carry and the intermediate output will determine the result for this column.

Perform a repeated AND with the carry to determine the result for the second column. The first AND between the two inputs will determine the intermediate output to the AND with the carry. The second AND between the carry and the intermediate output will determine the carry out for this column.

Repeat to get the result. After performing the same AND and XOR operations multiple times, you will have the result of the addition. Ignore the last carry. This is not needed for a fixed bit string.

Interpret the result of the addition. The result can be interpreted as an unsigned integer or as two's compliment. An unsigned integer has no sign. The values that can be represented by an n {\displaystyle n} n bit string is between 0 {\displaystyle 0} {\displaystyle 0} and 2 n − 1 {\displaystyle 2^{n-1}} {\displaystyle 2^{n-1}}. To convert the result back to decimal, perform 2 n − 1 ∗ i n + 2 n − 2 ∗ i n − 1 + . . . + 2 1 ∗ i 2 + 2 0 ∗ i 1 {\displaystyle 2^{n-1}*i_{n}+2^{n-2}*i_{n-1}+...+2^{1}*i_{2}+2^{0}*i_{1}} {\displaystyle 2^{n-1}*i_{n}+2^{n-2}*i_{n-1}+...+2^{1}*i_{2}+2^{0}*i_{1}}, where i n {\displaystyle i_{n}} {\displaystyle i_{n}} is the n {\displaystyle n} nth bit. A two's compliment integer has both negative and positive results. The values that can be represented by an n {\displaystyle n} n bit string is between − 2 n − 2 {\displaystyle -2^{n-2}} {\displaystyle -2^{n-2}} and 2 n − 2 {\displaystyle 2^{n-2}} {\displaystyle 2^{n-2}}. To convert the result back to decimal, first toggle all the bits then add 1 to the first bit if the last bit is on. Then use the same formula for computing the decimal result 2 n − 1 ∗ i n + 2 n − 2 ∗ i n − 1 + . . . + 2 1 ∗ i 2 + 2 0 ∗ i 1 {\displaystyle 2^{n-1}*i_{n}+2^{n-2}*i_{n-1}+...+2^{1}*i_{2}+2^{0}*i_{1}} {\displaystyle 2^{n-1}*i_{n}+2^{n-2}*i_{n-1}+...+2^{1}*i_{2}+2^{0}*i_{1}}, where i n {\displaystyle i_{n}} {\displaystyle i_{n}} is the n {\displaystyle n} nth bit. If you had to invert the bits, make sure to prepend a − sign before the answer.