views
Getting Started
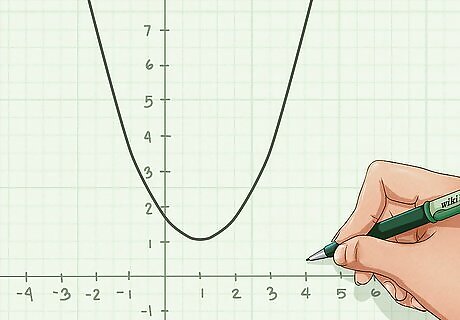
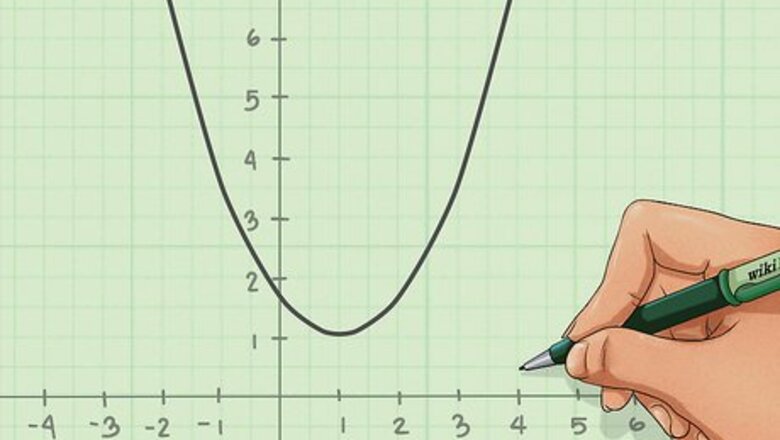
Select the parabola that you want to use. The parabola should be on a graph on a coordinate plane with x and y coordinates.
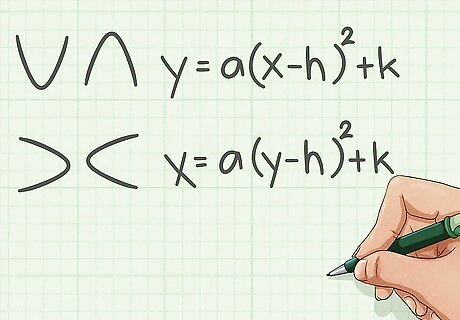
Remember the vertex form of a quadratic equation. The equation for parabolas that have openings facing the top and bottom use y = a ( x − h ) 2 + k {\displaystyle y=a(x-h)^{2}+k} y=a(x-h)^{2}+k. But if the parabola's opening faces the left or right, it will use x = a ( y − h ) 2 + k {\displaystyle x=a(y-h)^{2}+k} x=a(y-h)^{2}+k.

Note the coordinates of the vertex. There is only one vertex per parabola. The vertex is the point on the tip of the parabola.
Determining the Equation of a Parabola that Opens Upwards or Downwards

Replace h and k with the appropriate coordinates. The x coordinate of the vertex will replace h and the y coordinate will replace k.
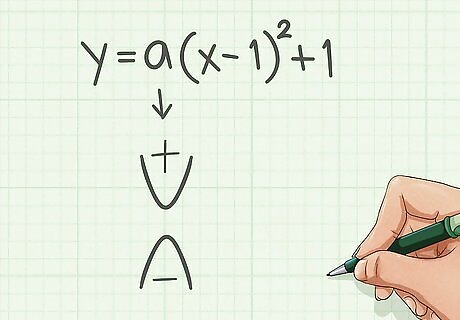
Find out if a is positive or negative. If the parabola is facing up , then a is positive. But if the parabola is facing down, a is negative.
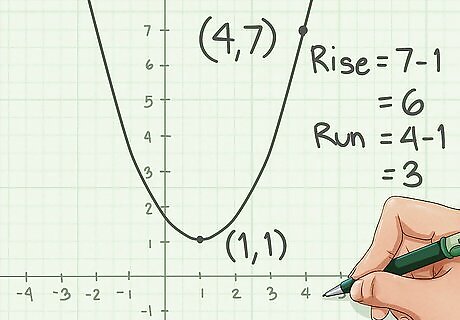
Find the next point from the vertex on the parabola that has coordinates with two integers (it doesn't matter whether it is to the left or the right). Find the rise and run between this point and the vertex. Examples of coordinates with two integers are: ( − 4 , 3 ) {\displaystyle (-4,3)} (-4,3), ( 0 , 2 ) {\displaystyle (0,2)} (0,2), and ( 9 , 9 ) {\displaystyle (9,9)} (9,9). Examples of coordinates without two integers are: ( 2.5 , − 1 ) {\displaystyle (2.5,-1)} (2.5,-1), ( 6.97 , 7.1 ) {\displaystyle (6.97,7.1)} (6.97,7.1), ( − 1.01 , 0 ) {\displaystyle (-1.01,0)} (-1.01,0). Remember that the rise is the difference in y and the run is the difference in x.
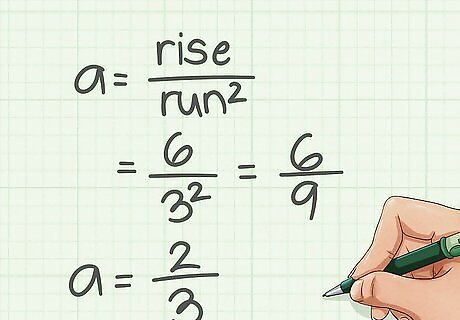
Find the value of a. Note the absolute value of the run. This will be the denominator of a. To find the numerator of a, simply divide the rise by the run. For example; if the rise is 2 and the run is 1, the denominator would be 1 and the numerator would be 2 divided by 1 which is 2. Thus, a would be 2. The process of finding a could be simplified to r i s e / r u n 2 {\displaystyle rise/run^{2}} rise/run^{2}.

Convert the equation to standard form if necessary. This might be handy if you have to factor it out properly. If you have y = ( x − 4 ) 2 + 4 {\displaystyle y=(x-4)^{2}+4} y=(x-4)^{2}+4, in standard form, it will be y = x 2 − 8 x + 20 {\displaystyle y=x^{2}-8x+20} y=x^{2}-8x+20 which could be factored neatly into y = ( x − 10 ) ( x + 2 ) {\displaystyle y=(x-10)(x+2)} y=(x-10)(x+2).
Determining the Equation of a Parabola that Opens Sideways
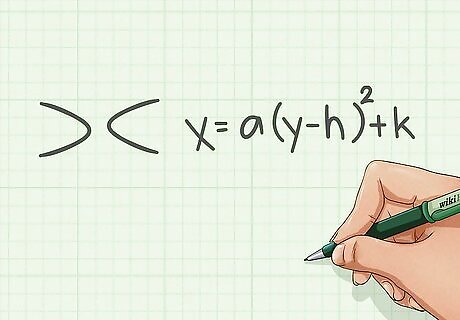
Remember to use the equation x = a ( y − h ) 2 + k {\displaystyle x=a(y-h)^{2}+k} x=a(y-h)^{2}+k since a parabola that opens sideways uses a different equation than a parabola that opens upwards or downwards.

Replace h and k with the appropriate coordinates. Replace h with the y coordinate of the vertex and k with the x coordinate. In the example shown in the picture, the vertex is the origin, (0, 0) so there will be no h and k, simplifying the equation to x = a y 2 {\displaystyle x=ay^{2}} x=ay^{2}.
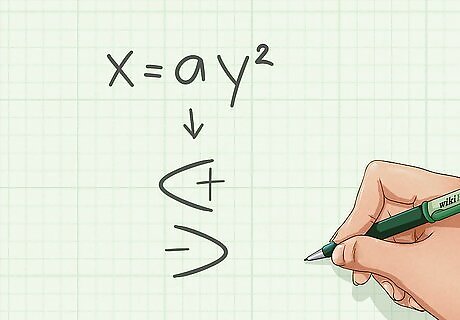
Determine if a is positive of negative. If the parabola opens to the right, a is positive. But if it opens to the left, then a is negative.
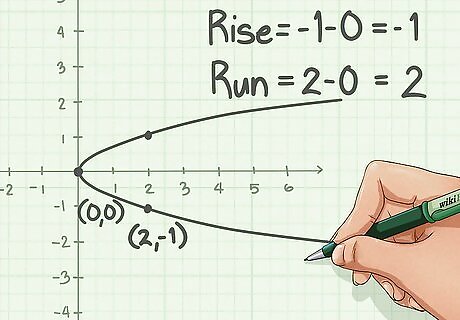
Find the next point from the vertex on the parabola that has coordinates with two integers. Calculate the rise and run between this point and the vertex.
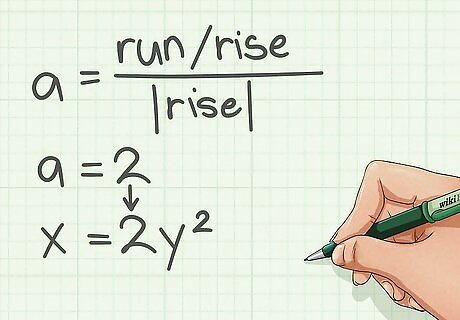
Find the value of a. Note the absolute value of the rise. This will be the denominator of a. To find the numerator of a, divide the run by the rise. If the rise is 5 and the run is 20, then a will be 4/5 because we can get 4 by dividing 20 and 5. Remember that a could also be calculated by dividing the rise by the run squared. But for a parabola that opens sideways, it is run divided by the rise squared.




















Comments
0 comment