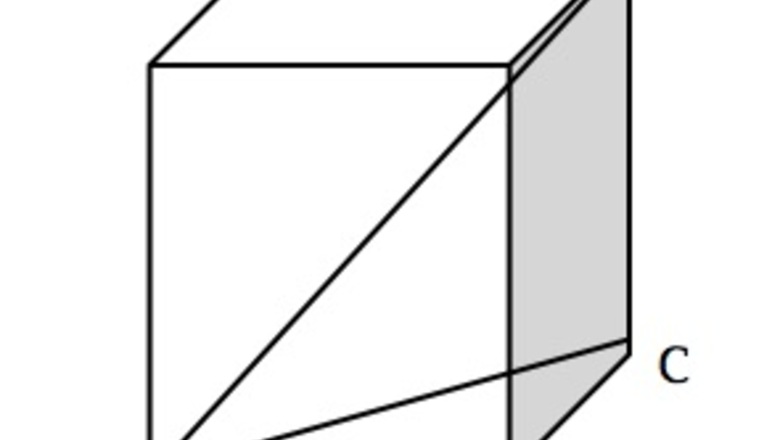
views
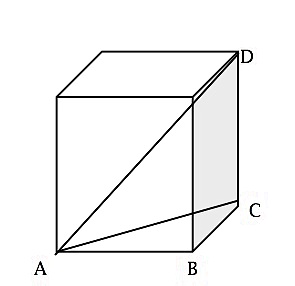
Sketch and label a diagram of a cube. Specify the long (internal) diagonal of a cube as line AD.

Open a new Excel workbook and worksheet and draw a unit-cube using the Media Browser "Shapes" tool option. That means that the length of the sides must be equal to 1 unit; that is side s = 1 unit. The six square shaped exterior surfaces (faces) are equal in dimensions, size, area and have the same shape. Therefore all faces are congruent.
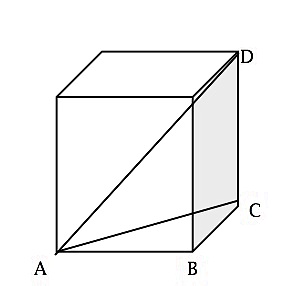
Label 3 consecutive corners (vertices) of the bottom face (the base) as A, B and C, thus forming triangle ABC. See the figure: label as point D the corner (vertex) above C, at the top of the cube. The segment CD is at a right angle (90 degrees) to the base.
Use the Pythagorean theorem: a + b = c, for the right triangle ABC where: ` Let [AB] + [BC] = [AC] Then let = [1] + [1] = 1 + 1 = 2, for the "left hand side" (LHS) = 2 thus: Examine the length of the RHS = AC squared: [AC] = 2. Let [AC] = [sqrt(2)]. Simplify that; you will find the length of the diagonal of the base, AC. We have AC = sqrt(2).
Find the length of the long internal diagonal by using the Pythagorean theorem for right triangle ACD: [AC] + [CD] = [AD], where AD is the long internal diagonal we seek. Use AC = sqrt(2) and knowing that CD = 1, we substitute these known values into the Pythagorean formula and have the following equation: [sqrt(2)] + 1 = [AD] Then let [sqrt(2)] + 1 = 2 + 1 = 3, then [AD] = [sqrt(3)]. Then realize that, [AD] the length of the internal diagonal from bottom to top and between opposing corners equals sqrt(3), because [sqrt(3)] = 3 (square root of the squared number) is just that number; let's call the number a, such as [sqrt(a)] = a ) and lengths are always positive numbers.
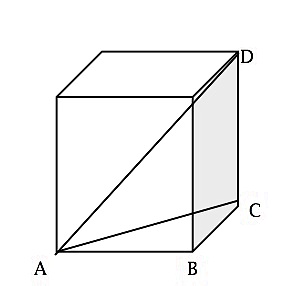
Find the internal diagonal of a cube with a different side length: modify the formula to side s equaling a different number, as not for the unit cube but any length of side s; so that each side of the triangle is a multiple of the parts of the unit cube: Let [s*AC] + [s*CD] = [s*AD] , by multiplication for sides of rt triangle ACD, and [s*sqrt(2)] + [s*1] = [s*sqrt(3)], by substitution. You also can modify the earlier formula to [s*AB] + [s*BC] = [s*AC]. [s*1] + [s*1] = [s*sqrt(2)], to convert from the unit cube with sides equaling 1, into a multiple of the sides of right triangle ABC with two legs = s*1, and its hypotenuse = s*sqrt(2). In both cases, the absolute value of s (your cube's side length) is used as the multiplier.Cube w Long Diagonal.jpg

















Comments
0 comment