
views
- Plug your numbers into the supply and demand equations:
- Qs = x + yP
- Qd = x - yP
- Use Qd = Qs to find the equilibrium price.
- Plug the price, or P, into either the supply equation or the demand equation to solve for equilibrium quantity.
Plug your numbers into the supply function.

The supply equation is Q s = x + y P {\displaystyle Qs=x+yP} {\displaystyle Qs=x+yP}. Q s {\displaystyle Qs} {\displaystyle Qs} is the units supplied, and X {\displaystyle X} X is the quantity, or amount, of units. P {\displaystyle P} P represents the price of each unit (typically in dollars). Look at your problem and plug in your numbers for the supply equation. For instance, let’s say that you are calculating the equilibrium quantity of calculators. The price of each calculator, or unit, is $5 ( P {\displaystyle P} P). At $5, the supplier can supply 2 calculators ( X {\displaystyle X} X). Therefore, your equation would be Q s = 2 + 5 P {\displaystyle Qs=2+5P} {\displaystyle Qs=2+5P}
Insert the demand into the demand function.

The demand equation is Q d = x − y P {\displaystyle Qd=x-yP} {\displaystyle Qd=x-yP}. Q d {\displaystyle Qd} {\displaystyle Qd} is the number of demanded units. In this equation, X {\displaystyle X} X is the quantity and P {\displaystyle P} P is still the price of your unit in dollars. Take a look at your problem and plug in the numbers to the demand function. Continuing our example from above, let’s say that the price of a calculator is $2 ( P {\displaystyle P} P), and the demand for a calculator at that price is 16 ( X {\displaystyle X} X). The demand equation would be Q d = 16 − 2 P {\displaystyle Qd=16-2P} {\displaystyle Qd=16-2P}.
Set the 2 quantities as equal in price.
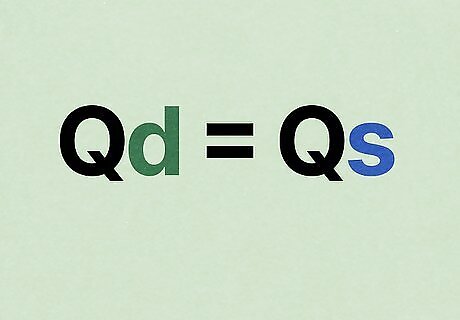
Use Q d = Q s {\displaystyle Qd=Qs} {\displaystyle Qd=Qs} to find the equilibrium. Picture your supply and demand plotted on a graph. The equilibrium point would be when the 2 lines cross over each other in the center of the graph. In order to find that point, we need to assume that the supply equals the demand, or that Q d = Q s {\displaystyle Qd=Qs} {\displaystyle Qd=Qs}. Plug your numbers into the equation. Our new equation would look like this: 16 − 2 P = 2 + 5 P {\displaystyle 16-2P=2+5P} {\displaystyle 16-2P=2+5P}.
Isolate the variable to solve the equation.

Solve the equation to find the equilibrium price. To isolate the variable, add the Q d {\displaystyle Qd} {\displaystyle Qd} price ( P {\displaystyle P} P) to both sides. Then, subtract the Q s {\displaystyle Qs} {\displaystyle Qs} quantity ( X {\displaystyle X} X) from both sides. For example: 16 − 2 P = 2 + 5 P {\displaystyle 16-2P=2+5P} {\displaystyle 16-2P=2+5P} ( 16 − 2 ) − ( 2 P + − 2 P ) = ( 2 − 2 ) + ( 5 P + 2 P ) {\displaystyle (16-2)-(2P+-2P)=(2-2)+(5P+2P)} {\displaystyle (16-2)-(2P+-2P)=(2-2)+(5P+2P)} ( 16 − 2 ) = ( 5 P + 2 P ) {\displaystyle (16-2)=(5P+2P)} {\displaystyle (16-2)=(5P+2P)} 14 = 7 P {\displaystyle 14=7P} {\displaystyle 14=7P}
Simplify the equation by dividing both sides.
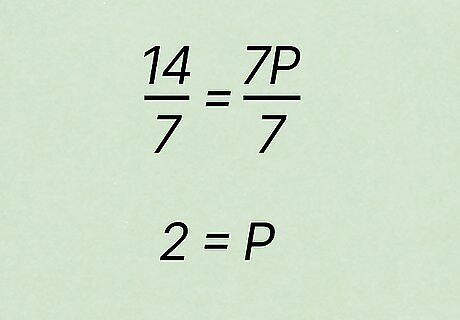
Solve for P {\displaystyle P} P by dividing each side of the equation. You’re almost there! To find the price, or P {\displaystyle P} P, divide each side to simplify your equation. 14 / 7 = 7 P / 7 {\displaystyle 14/7=7P/7} {\displaystyle 14/7=7P/7} 2 = P {\displaystyle 2=P} {\displaystyle 2=P} You now know that the equilibrium price, or the price where Q d = Q s {\displaystyle Qd=Qs} {\displaystyle Qd=Qs}, is $2.
Insert the P value and solve to find the equilibrium quantity.
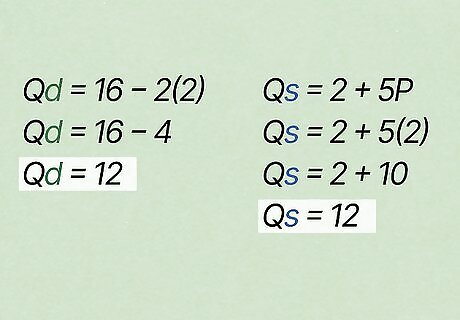
Plug the equilibrium price into the equation and solve. You can choose either the demand equation or the supply equation (since both are equal, they will both give you the same answer). In the example below, we will use the demand equation, which is Q d = 16 − 2 P {\displaystyle Qd=16-2P} {\displaystyle Qd=16-2P}. Take the price, P, (which we now know is $2), and plug it into the equation. Q d = 16 − 2 ( 2 ) {\displaystyle Qd=16-2(2)} {\displaystyle Qd=16-2(2)} Q d = 16 − 4 {\displaystyle Qd=16-4} {\displaystyle Qd=16-4} Q d = 12 {\displaystyle Qd=12} {\displaystyle Qd=12} You now know that the equilibrium quantity is 12, which means that at $2 per calculator, consumers will purchase 12 of them. To use the supply equation, your answer would be: Q s = 2 + 5 P {\displaystyle Qs=2+5P} {\displaystyle Qs=2+5P} Q s = 2 + 5 ( 2 ) {\displaystyle Qs=2+5(2)} {\displaystyle Qs=2+5(2)} Q s = 2 + 10 {\displaystyle Qs=2+10} {\displaystyle Qs=2+10} Q s = 12 {\displaystyle Qs=12} {\displaystyle Qs=12}
















Comments
0 comment