How to Factor the Difference of Two Perfect Squares

Evaluating the Polynomial

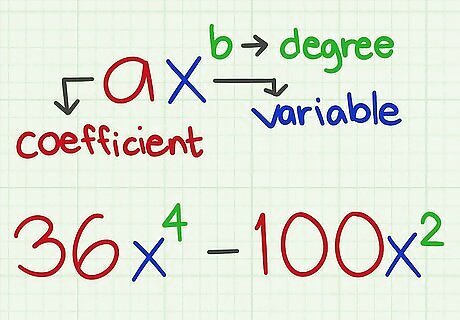
Identify the coefficient, variable, and degree of each term. A coefficient is the number in front of a variable, which is multiplied by the variable. The variable is the unknown value, usually denoted by x {\displaystyle x} x or y {\displaystyle y} y.. The degree refers to the exponent of the variable. For example, a second-degree term has a value to the second power ( x 2 {\displaystyle x^{2}} x^{{2}}) and a fourth-degree term has a value to the fourth power ( x 4 {\displaystyle x^{4}} x^{{4}}). For example, in the polynomial 36 x 4 − 100 x 2 {\displaystyle 36x^{4}-100x^{2}} 36x^{{4}}-100x^{{2}}, the coefficients are 36 {\displaystyle 36} 36 and 100 {\displaystyle 100} 100, the variable is x {\displaystyle x} x, and the first term ( 36 x 4 {\displaystyle 36x^{4}} 36x^{{4}}) is a fourth-degree term, and the second term ( 100 x 2 {\displaystyle 100x^{2}} 100x^{{2}}) is a second-degree term.

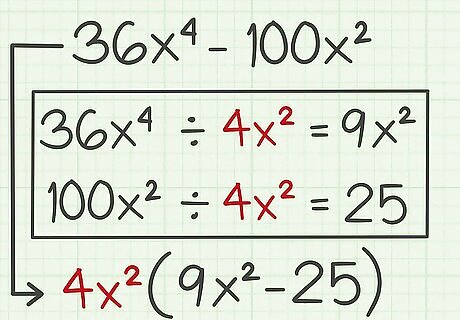
Look for a greatest common factor. A greatest common factor is the highest factor that divides evenly into two or more terms. If there is a factor common to both terms of the polynomial, factor this out. For example, the two terms in the polynomial 36 x 4 − 100 x 2 {\displaystyle 36x^{4}-100x^{2}} 36x^{{4}}-100x^{{2}} have a greatest common factor of 4 x 2 {\displaystyle 4x^{2}} 4x^{{2}}. Factoring this out, the problem becomes 4 x 2 ( 9 x 2 − 25 ) {\displaystyle 4x^{2}(9x^{2}-25)} 4x^{{2}}(9x^{{2}}-25) .

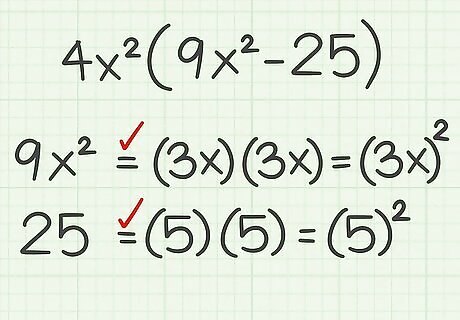
Determine whether the terms are perfect squares. If you factored out a greatest common factor, you are only looking at the terms that remain inside the parentheses. A perfect square is the result of multiplying an integer by itself. A variable is a perfect square if its exponent is an even number. You can only factor using the difference of squares if each term in the polynomial is a perfect square. For example, 9 x 2 {\displaystyle 9x^{2}} 9x^{{2}} is a perfect square, because ( 3 x ) ( 3 x ) = 9 x 2 {\displaystyle (3x)(3x)=9x^{2}} (3x)(3x)=9x^{{2}}. The number 25 {\displaystyle 25} 25 is also a perfect square, because ( 5 ) ( 5 ) = 25 {\displaystyle (5)(5)=25} (5)(5)=25. Thus, you can factor 9 x 2 − 25 {\displaystyle 9x^{2}-25} 9x^{{2}}-25 using the difference of squares formula.

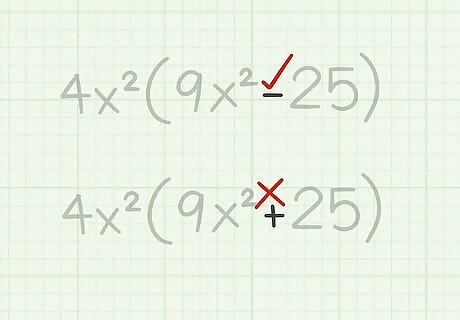
Make sure you are finding the difference. You know you are finding the difference if you have a polynomial that subtracts one term from another. The difference of squares only applies to these polynomials, and not those in which addition is used. For example, you cannot factor 9 x 2 + 25 {\displaystyle 9x^{2}+25} 9x^{{2}}+25 using the difference of squares formula, because in this polynomial you are finding a sum, not a difference.

Using the Formula

Set up the formula for the difference of squares. The formula is a 2 − b 2 = ( a − b ) ( a + b ) {\displaystyle a^{2}-b^{2}=(a-b)(a+b)} a^{{2}}-b^{{2}}=(a-b)(a+b). The terms a 2 {\displaystyle a^{2}} a^{{2}} and b 2 {\displaystyle b^{2}} b^{{2}} are the perfect squares in your polynomial, and a {\displaystyle a} a and b {\displaystyle b} b are the roots of the perfect squares.

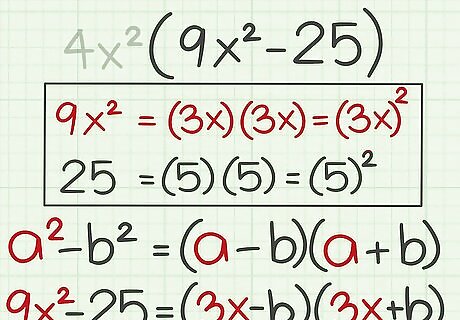
Plug the first term into the formula. This is the value for a {\displaystyle a} a. To find this value, take the square root of the first perfect square in the polynomial. Remember that a square root of a number is a factor you multiply by itself to get that number. For example, since ( 3 x ) ( 3 x ) = 9 x 2 {\displaystyle (3x)(3x)=9x^{2}} (3x)(3x)=9x^{{2}}, the square root of 9 x 2 {\displaystyle 9x^{2}} 9x^{{2}} is 3 x {\displaystyle 3x} 3x. So you should substitute this value for a {\displaystyle a} a in the difference of squares formula: 9 x 2 − 25 = ( 3 x − b ) ( 3 x + b ) {\displaystyle 9x^{2}-25=(3x-b)(3x+b)} 9x^{{2}}-25=(3x-b)(3x+b).

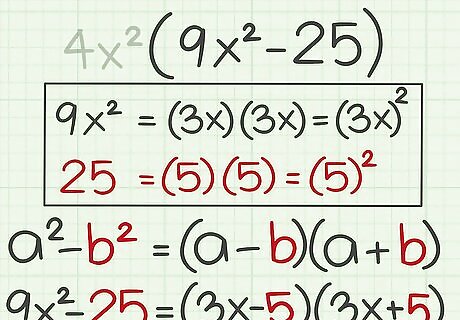
Plug the second term into the formula. This is the value for b {\displaystyle b} b, which is the square root of the second term in the polynomial. For example, since ( 5 ) ( 5 ) = 25 {\displaystyle (5)(5)=25} (5)(5)=25, the square root of 25 {\displaystyle 25} 25 is 5 {\displaystyle 5} 5. So you should substitute this value for b {\displaystyle b} b in the difference of squares formula: 9 x 2 − 25 = ( 3 x − 5 ) ( 3 x + 5 ) {\displaystyle 9x^{2}-25=(3x-5)(3x+5)} 9x^{{2}}-25=(3x-5)(3x+5).

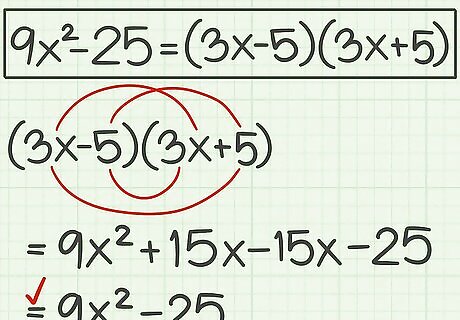
Check your work. Use the FOIL method to multiply the two factors. If your result is your original polynomial, you know you have factored correctly. For example: ( 3 x − 5 ) ( 3 x + 5 ) {\displaystyle (3x-5)(3x+5)} (3x-5)(3x+5) = 9 x 2 + 15 x − 15 x − 25 {\displaystyle =9x^{2}+15x-15x-25} =9x^{{2}}+15x-15x-25 = 9 x 2 − 25 {\displaystyle =9x^{2}-25} =9x^{{2}}-25.

Solving Practice Problems

Factor this polynomial. Use the difference of two squares formula: 36 x 4 − 9 {\displaystyle 36x^{4}-9} 36x^{{4}}-9. The terms have no greatest common factor, so there is no need to factor anything out of the polynomial. The term 36 x 4 {\displaystyle 36x^{4}} 36x^{{4}} is a perfect square, since ( 6 x 2 ) ( 6 x 2 ) = 36 x 4 {\displaystyle (6x^{2})(6x^{2})=36x^{4}} (6x^{{2}})(6x^{{2}})=36x^{{4}}. The term 9 {\displaystyle 9} 9 is a perfect square, since ( 3 ) ( 3 ) = 9 {\displaystyle (3)(3)=9} (3)(3)=9. The difference of squares formula is a 2 − b 2 = ( a − b ) ( a + b ) {\displaystyle a^{2}-b^{2}=(a-b)(a+b)} a^{{2}}-b^{{2}}=(a-b)(a+b). Thus, 36 x 4 − 9 = ( a − b ) ( a + b ) {\displaystyle 36x^{4}-9=(a-b)(a+b)} 36x^{{4}}-9=(a-b)(a+b), where a {\displaystyle a} a and b {\displaystyle b} b are the square roots of the perfect squares. The square root of 36 x 4 {\displaystyle 36x^{4}} 36x^{{4}} is 6 x 2 {\displaystyle 6x^{2}} 6x^{{2}}. Plugging in for a {\displaystyle a} a you have 36 x 4 − 9 = ( 6 x 2 − b ) ( 6 x 2 + b ) {\displaystyle 36x^{4}-9=(6x^{2}-b)(6x^{2}+b)} 36x^{{4}}-9=(6x^{{2}}-b)(6x^{{2}}+b). The square root of 9 {\displaystyle 9} 9 is 3 {\displaystyle 3} 3. So plugging in for b {\displaystyle b} b, you have 36 x 4 − 9 = ( 6 x 2 − 3 ) ( 6 x 2 + 3 ) {\displaystyle 36x^{4}-9=(6x^{2}-3)(6x^{2}+3)} 36x^{{4}}-9=(6x^{{2}}-3)(6x^{{2}}+3).

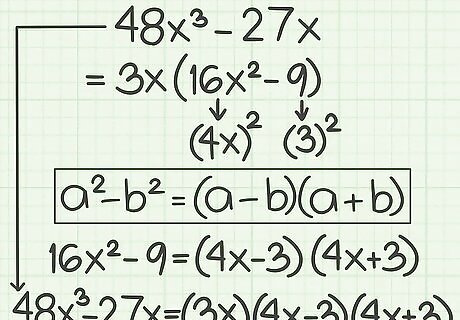
Try factoring this polynomial. Make sure you factor out a greatest common factor, and use the difference of two squares: 48 x 3 − 27 x {\displaystyle 48x^{3}-27x} 48x^{{3}}-27x. Find the greatest common factor of each term. This term is 3 x {\displaystyle 3x} 3x, so factor this out of the polynomial: 3 x ( 16 x 2 − 9 ) {\displaystyle 3x(16x^{2}-9)} 3x(16x^{{2}}-9). The term 16 x 2 {\displaystyle 16x^{2}} 16x^{{2}} is a perfect square, since ( 4 x ) ( 4 x ) = 16 x 2 {\displaystyle (4x)(4x)=16x^{2}} (4x)(4x)=16x^{{2}}. The term 9 {\displaystyle 9} 9 is a perfect square, since ( 3 ) ( 3 ) = 9 {\displaystyle (3)(3)=9} (3)(3)=9. The difference of squares formula is a 2 − b 2 = ( a − b ) ( a + b ) {\displaystyle a^{2}-b^{2}=(a-b)(a+b)} a^{{2}}-b^{{2}}=(a-b)(a+b). Thus, 48 x 3 − 27 x = 3 x ( a − b ) ( a + b ) {\displaystyle 48x^{3}-27x=3x(a-b)(a+b)} 48x^{{3}}-27x=3x(a-b)(a+b), where a {\displaystyle a} a and b {\displaystyle b} b are the square roots of the perfect squares. The square root of 16 x 2 {\displaystyle 16x^{2}} 16x^{{2}} is 4 x {\displaystyle 4x} 4x. Plugging in for a {\displaystyle a} a you have 48 x 3 − 27 x = 3 x ( 4 x − b ) ( 4 x + b ) {\displaystyle 48x^{3}-27x=3x(4x-b)(4x+b)} 48x^{{3}}-27x=3x(4x-b)(4x+b). The square root of 9 {\displaystyle 9} 9 is 3 {\displaystyle 3} 3. So plugging in for b {\displaystyle b} b, you have 48 x 3 − 27 x = 3 x ( 4 x − 3 ) ( 4 x + 3 ) {\displaystyle 48x^{3}-27x=3x(4x-3)(4x+3)} 48x^{{3}}-27x=3x(4x-3)(4x+3).

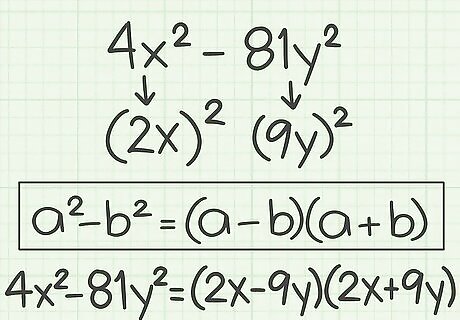
Factor the following polynomial. It has two variables, but it still follows the rules for the difference of squares method: 4 x 2 − 81 y 2 {\displaystyle 4x^{2}-81y^{2}} 4x^{{2}}-81y^{{2}}. No factor is common to each term in this polynomial, so there is nothing to factor out before you begin factoring the difference of squares. The term 4 x 2 {\displaystyle 4x^{2}} 4x^{{2}} is a perfect square, since ( 2 x ) ( 2 x ) = 4 x 2 {\displaystyle (2x)(2x)=4x^{2}} (2x)(2x)=4x^{{2}}. The term 81 y 2 {\displaystyle 81y^{2}} 81y^{{2}} is a perfect square, since ( 9 y ) ( 9 y ) = 81 y 2 {\displaystyle (9y)(9y)=81y^{2}} (9y)(9y)=81y^{{2}}. The difference of squares formula is a 2 − b 2 = ( a − b ) ( a + b ) {\displaystyle a^{2}-b^{2}=(a-b)(a+b)} a^{{2}}-b^{{2}}=(a-b)(a+b). Thus, 4 x 2 − 81 y 2 = ( a − b ) ( a + b ) {\displaystyle 4x^{2}-81y^{2}=(a-b)(a+b)} 4x^{{2}}-81y^{{2}}=(a-b)(a+b), where a {\displaystyle a} a and b {\displaystyle b} b are the square roots of the perfect squares. The square root of 4 x 2 {\displaystyle 4x^{2}} 4x^{{2}} is 2 x {\displaystyle 2x} 2x. Plugging in for a {\displaystyle a} a you have 4 x 2 − 81 y 2 = ( 2 x − b ) ( 2 x + b ) {\displaystyle 4x^{2}-81y^{2}=(2x-b)(2x+b)} 4x^{{2}}-81y^{{2}}=(2x-b)(2x+b). The square root of 81 y 2 {\displaystyle 81y^{2}} 81y^{{2}} is 9 y {\displaystyle 9y} 9y. So plugging in for b {\displaystyle b} b, you have 4 x 2 − 81 y 2 = ( 2 x − 9 y ) ( 2 x + 9 y ) {\displaystyle 4x^{2}-81y^{2}=(2x-9y)(2x+9y)} 4x^{{2}}-81y^{{2}}=(2x-9y)(2x+9y).