views
Converting to a Decimal
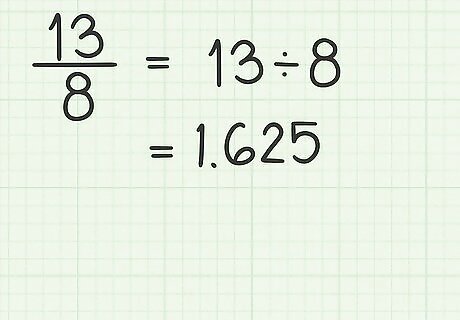
Use a calculator to divide the numerator by the denominator. The numerator is the top number, and the denominator is the bottom number. It is best to use a calculator, because depending on the fraction, you might end up with a number that has many decimal places. Completing this calculation converts the fraction to a decimal. Note that, because you have an improper fraction, the denominator will divide into the numerator at least 1 whole time. That means that your decimal will be greater than 1. It also means that your percent will be greater than 100%. For example, if you are converting 13 8 {\displaystyle {\frac {13}{8}}} {\frac {13}{8}}, you would calculate 13 ÷ 8 = 1.625 {\displaystyle 13\div 8=1.625} 13\div 8=1.625.
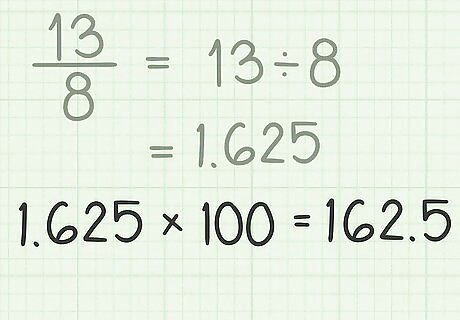
Multiply the decimal by 100. You can do this with a calculator, but an easy way to do this in your head is to simply move the decimal point two places to the right. For example, 1.625 × 100 = 162.5 {\displaystyle 1.625\times 100=162.5} 1.625\times 100=162.5.
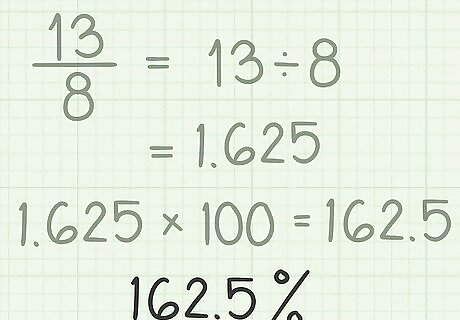
Add a percent sign. Until you add a percent sign, your number still reads like a decimal, even though it no longer is. So, add your percent sign to avoid confusion. The percent sign comes after the number. For example, 162.5 % {\displaystyle 162.5\%} 162.5\%.
Multiplying by 100
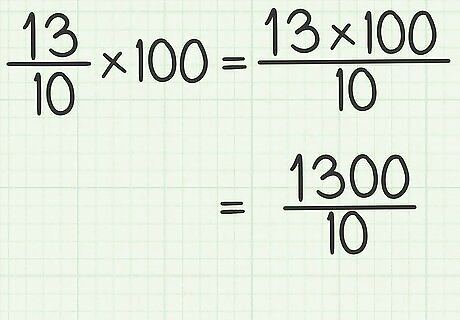
Multiply the fraction by 100. To multiply a fraction by 100, multiply the numerator by 100. Keep the same denominator. You can also think of multiplying the fraction by 100 1 {\displaystyle {\frac {100}{1}}} {\frac {100}{1}}. Note that 100 ÷ 1 = 100 {\displaystyle 100\div 1=100} 100\div 1=100, so 100 1 = 100 {\displaystyle {\frac {100}{1}}=100} {\frac {100}{1}}=100. It doesn’t matter if you multiply by the whole number or the fraction, since they mean the same thing. For example: 13 10 × 100 {\displaystyle {\frac {13}{10}}\times 100} {\frac {13}{10}}\times 100 13 × 100 10 {\displaystyle {\frac {13\times 100}{10}}} {\frac {13\times 100}{10}} 1300 10 {\displaystyle {\frac {1300}{10}}} {\frac {1300}{10}}
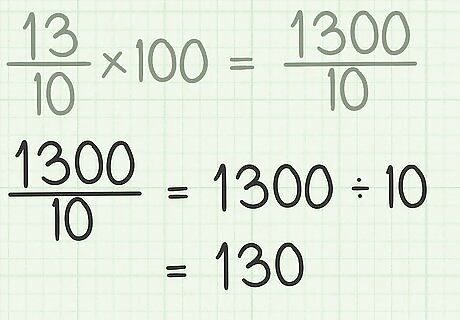
Divide the numerator by the denominator. The numerator is the top number, the denominator is the bottom number. You will likely need a calculator to do this, or you can do it manually. For example, 1300 ÷ 10 = 130 {\displaystyle 1300\div 10=130} 1300\div 10=130.
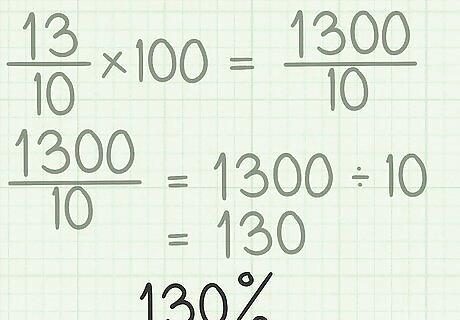
Add a percent sign. The percent sign goes after the number, and helps avoid confusion. Remember that a percent is not the same thing as a decimal or whole number, so you need to denote a percent with the appropriate sign. For example, 130 % {\displaystyle 130\%} 130\%
Finding an Equivalent Fraction
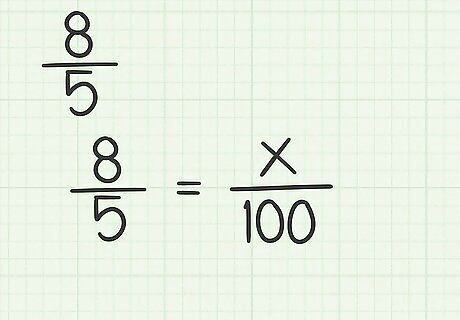
Understand what a percent looks like as a fraction. Since a percent is equal to a certain number of hundredths, you are going to convert the fraction to an equivalent one with 100 in the denominator. For example, if you have 8 5 {\displaystyle {\frac {8}{5}}} {\frac {8}{5}}, you want to find x {\displaystyle x} x in the equation 8 5 = x 100 {\displaystyle {\frac {8}{5}}={\frac {x}{100}}} {\frac {8}{5}}={\frac {x}{100}}.
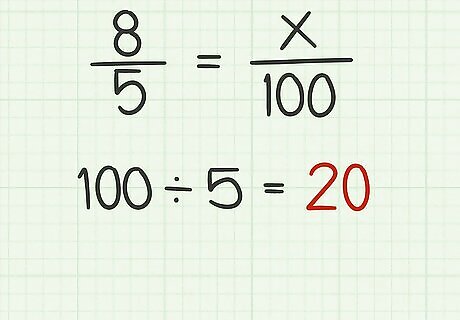
Divide 100 by the denominator of the fraction. Remember that the denominator is the bottom number. This calculation will give you a factor of change telling you how much bigger 100 is than the denominator. Note that this method only works if the denominator divides evenly into 100. For example, if you are converting 8 5 {\displaystyle {\frac {8}{5}}} {\frac {8}{5}}, you would calculate 100 ÷ 5 = 20 {\displaystyle 100\div 5=20} 100\div 5=20. So, a denominator of 100 is 20 times bigger than a denominator of 5.
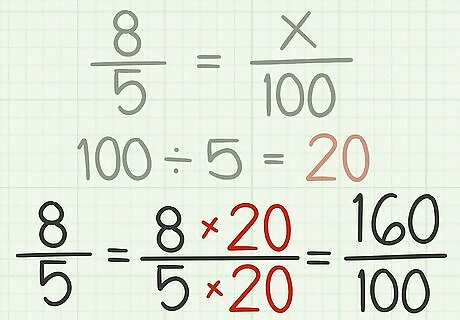
Multiply the numerator and denominator by the factor of change. To maintain an equivalent fraction, whatever you do to the original denominator, you must also do to the numerator. For example, 8 5 = 8 × 20 5 × 20 = 160 100 {\displaystyle {\frac {8}{5}}={\frac {8\times 20}{5\times 20}}={\frac {160}{100}}} {\frac {8}{5}}={\frac {8\times 20}{5\times 20}}={\frac {160}{100}}.
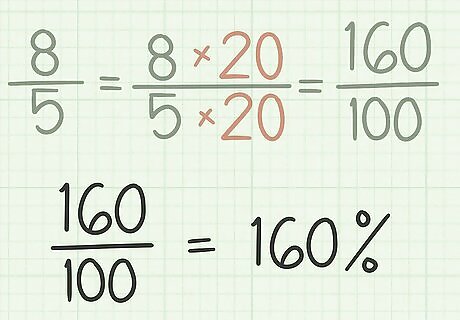
State the fraction as a percent. Remember that a percent is simply a number out of 100, or hundredths. Since your fraction is now shown as x 100 {\displaystyle {\frac {x}{100}}} {\frac {x}{100}}, the numerator of your fraction is now the percent. Note that, since you are working with an improper fraction, your numerator is larger than your denominator. This means that your fraction represents more than 100 percent. Don’t forget to include the percent sign after the number. For example, 160 100 = 160 % {\displaystyle {\frac {160}{100}}=160\%} {\frac {160}{100}}=160\%

















Comments
0 comment