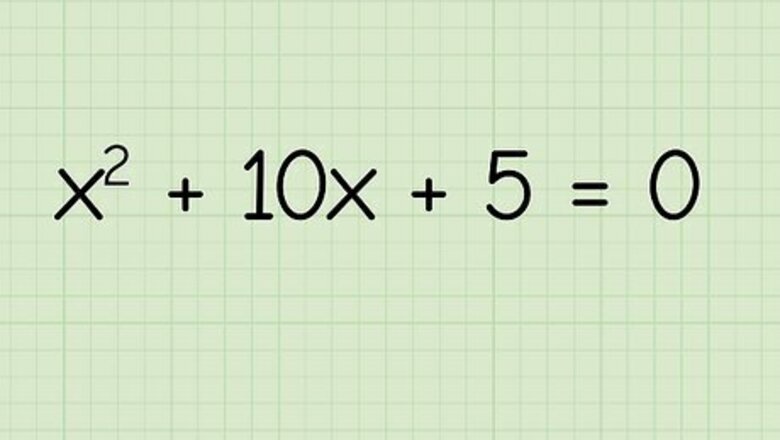
views
Completing the Square
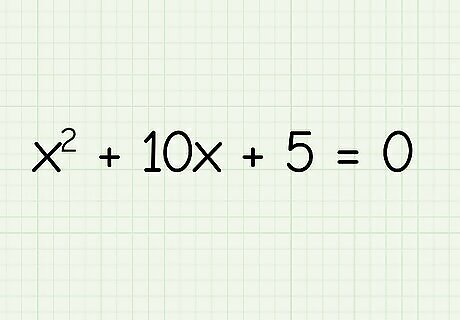
Write down the equation. Let's say you're working with the following equation: x 2 + 10 x + 5 = 0. {\displaystyle x^{2}+10x+5=0.} {\displaystyle x^{2}+10x+5=0.}
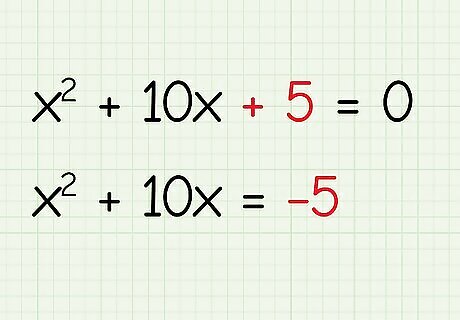
Subtract the last term from both sides of the equation. To isolate your x terms, move the constant (number without an “x”) to the other side of the equation by subtracting it from both sides. x 2 + 10 x = − 5. {\displaystyle x^{2}+10x=-5.} {\displaystyle x^{2}+10x=-5.}
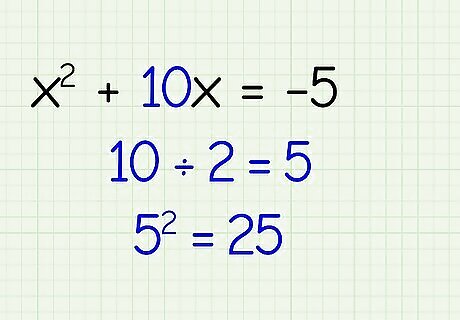
Halve the coefficient of the x term and square it. Take the number in front of the x (second) term in the equation, divide it by 2, and then square it. In this example, the second term is 10x, so 10 2 = 5 , 5 2 = 25 {\displaystyle {\frac {10}{2}}=5,5^{2}=25} {\displaystyle {\frac {10}{2}}=5,5^{2}=25}.
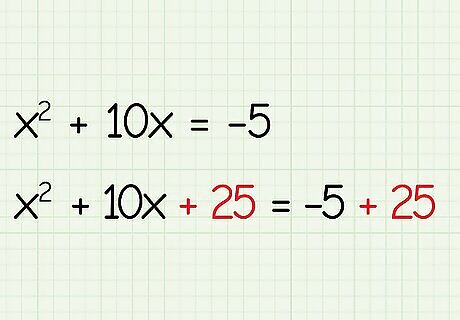
Add the term to both sides of the equation. By adding this term to the left side of the equation, you create a polynomial that is a perfect square. To keep the equation balanced, add the number to the right side of the equation, as well. x 2 + 10 x + 25 = − 5 + 25. {\displaystyle x^{2}+10x+25=-5+25.} {\displaystyle x^{2}+10x+25=-5+25.}
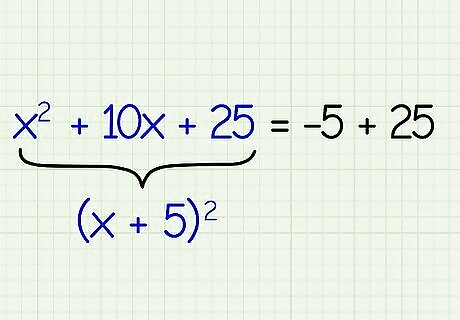
Factor the left side of the equation. Now that the left side is a perfect square, you can rewrite it as (x + the halved second term), or ( x + 5 ) 2 {\displaystyle (x+5)^{2}} {\displaystyle (x+5)^{2}} for this example. You can check your math by multiplying it out and seeing if it gives you the first three terms from the last step.
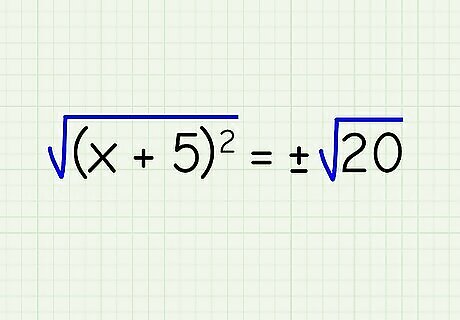
Take the square root of both sides. To solve your equation, undo the square on the left by taking the square root of both sides. ( x + 5 ) 2 = {\displaystyle {\sqrt {(x+5)^{2}}}=} {\displaystyle {\sqrt {(x+5)^{2}}}=} ± 20 {\displaystyle {\sqrt {20}}} {\sqrt {20}}.
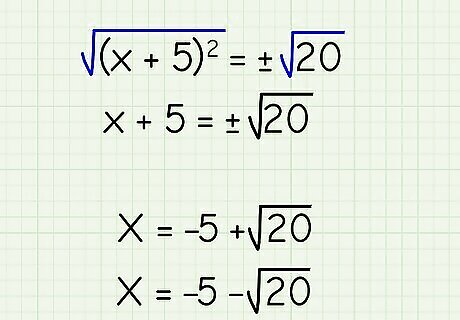
Solve to find the roots of the equation. When you take the square root of the right side of the equation, the result is both negative and positive, since negative numbers are also positive when they’re squared. To solve this equation, break it into two parts: x = − 5 + 20 , x = − 5 − 20 {\displaystyle x=-5+{\sqrt {20}},x=-5-{\sqrt {20}}} {\displaystyle x=-5+{\sqrt {20}},x=-5-{\sqrt {20}}}.
Writing Vertex Form by Completing the Square
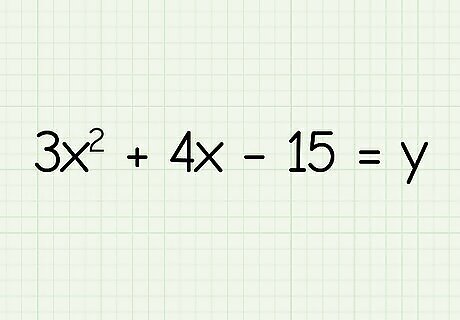
Write your equation. For this example, try an equation where the x 2 {\displaystyle x^{2}} x^{{2}} term has a coefficient, like 3 x 2 + 4 x − 15 = y {\displaystyle 3x^{2}+4x-15=y} {\displaystyle 3x^{2}+4x-15=y}. Vertex form is a way of writing a quadratic equation ( a x 2 + b x + C {\displaystyle ax^{2}+bx+C} {\displaystyle ax^{2}+bx+C}) with the coordinates of the vertex of the parabola formed by that equation. Vertex form is written as f ( x ) = a ( x − h ) 2 + k {\displaystyle f(x)=a(x-h)^{2}+k} {\displaystyle f(x)=a(x-h)^{2}+k} where (h, k) is the vertex of a parabola.
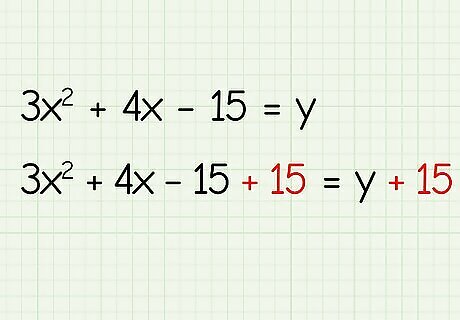
Move the constant to the right side of the equation. Isolate the x terms by adding 15 to both sides of the equation. 3 x 2 + 4 x − 15 + 15 = y + 15 {\displaystyle 3x^{2}+4x-15+15=y+15} {\displaystyle 3x^{2}+4x-15+15=y+15}
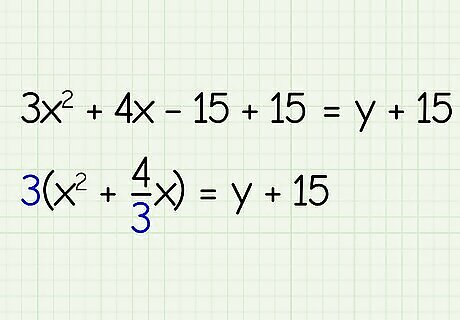
Factor out the coefficient of the squared term from the first 2 terms. To complete the square, the leading coefficient has to be 1, so factor 3 out of the left side of the equation. 3 ( x 2 + 4 3 x ) = y + 15 {\displaystyle 3(x^{2}+{\frac {4}{3}}x)=y+15} {\displaystyle 3(x^{2}+{\frac {4}{3}}x)=y+15}.
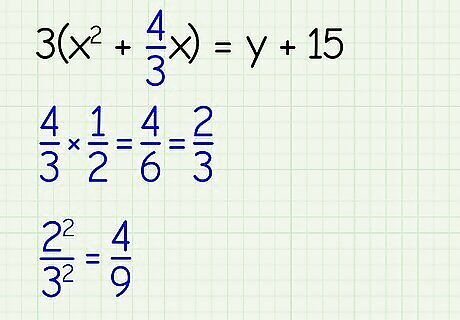
Halve the second term and square it. The second term, also known as the b term, in the equation, is 4 3 {\displaystyle {\frac {4}{3}}} {\frac {4}{3}}. First, divide it by two: 4 3 ∗ 1 2 = 4 6 = 2 3 {\displaystyle {\frac {4}{3}}*{\frac {1}{2}}={\frac {4}{6}}={\frac {2}{3}}} {\displaystyle {\frac {4}{3}}*{\frac {1}{2}}={\frac {4}{6}}={\frac {2}{3}}}. Then, square the term: 2 2 3 2 = 4 9 {\displaystyle {\frac {2^{2}}{3^{2}}}={\frac {4}{9}}} {\displaystyle {\frac {2^{2}}{3^{2}}}={\frac {4}{9}}}. Completing the square refers to finding a constant “C” that you can add to the first two terms to make a perfect square trinomial, which can be factored into the expression ( x + a ) 2 {\displaystyle (x+a)^{2}} {\displaystyle (x+a)^{2}}. The number you get at this step is the constant that completes the square.
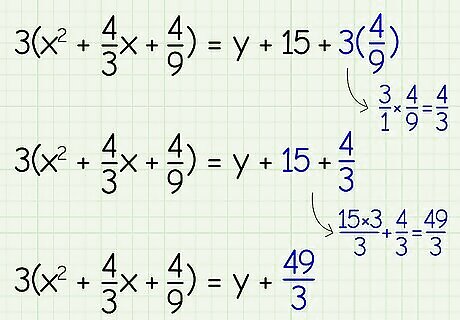
Add the term to both sides of the equation. Use the new term to make a perfect square trinomial by adding it into the parentheses. Since you factored out a 3, multiply the new term by three before adding it to the right side of the equation with the y term. 3 ( x 2 + 4 3 x + 4 9 ) = y + 15 + 3 ( 4 9 ) = {\displaystyle 3(x^{2}+{\frac {4}{3}}x+{\frac {4}{9}})=y+15+3({\frac {4}{9}})=} {\displaystyle 3(x^{2}+{\frac {4}{3}}x+{\frac {4}{9}})=y+15+3({\frac {4}{9}})=} 3 ( x 2 + 4 3 x + 4 9 ) = y + 15 + 4 3 = {\displaystyle 3(x^{2}+{\frac {4}{3}}x+{\frac {4}{9}})=y+15+{\frac {4}{3}}=} {\displaystyle 3(x^{2}+{\frac {4}{3}}x+{\frac {4}{9}})=y+15+{\frac {4}{3}}=} 3 ( x 2 + 4 3 x + 4 9 ) = y + 49 3 {\displaystyle 3(x^{2}+{\frac {4}{3}}x+{\frac {4}{9}})=y+{\frac {49}{3}}} {\displaystyle 3(x^{2}+{\frac {4}{3}}x+{\frac {4}{9}})=y+{\frac {49}{3}}}

Factor the trinomial as a square and isolate “y.” Now that you have a perfect square in the parenthesis, factor it out using the halved b term from before, in this case 2 3 {\displaystyle {\frac {2}{3}}} {\frac {2}{3}}. Write your equation as a factored square, subtract the constant from the y side, and add it to the x side. 3 ( x + 2 3 ) 2 − 49 3 = y + 49 3 − 49 3 {\displaystyle 3(x+{\frac {2}{3}})^{2}-{\frac {49}{3}}=y+{\frac {49}{3}}-{\frac {49}{3}}} {\displaystyle 3(x+{\frac {2}{3}})^{2}-{\frac {49}{3}}=y+{\frac {49}{3}}-{\frac {49}{3}}} 3 ( x + 2 3 ) 2 − 49 3 = y {\displaystyle 3(x+{\frac {2}{3}})^{2}-{\frac {49}{3}}=y} {\displaystyle 3(x+{\frac {2}{3}})^{2}-{\frac {49}{3}}=y} If you’re using the vertex form f ( x ) = a ( x − h ) 2 + k {\displaystyle f(x)=a(x-h)^{2}+k} {\displaystyle f(x)=a(x-h)^{2}+k} to find the vertex of a parabola (h, k), remember that “h” has to be negative and “k” has to be positive. In this example, the vertex is ( − 2 3 , − 49 3 ) {\displaystyle (-{\frac {2}{3}},-{\frac {49}{3}})} {\displaystyle (-{\frac {2}{3}},-{\frac {49}{3}})}.
Solving Quadratic Equations
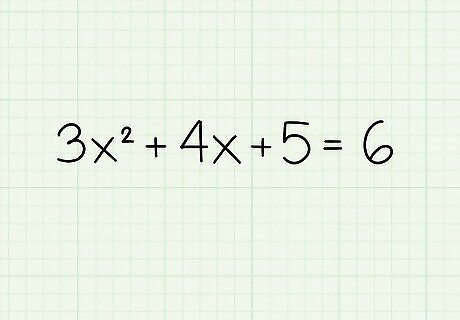
Write down the problem. Let's say you're working with the following equation: 3 x 2 + 4 x + 5 = 6 {\displaystyle 3x^{2}+4x+5=6} {\displaystyle 3x^{2}+4x+5=6}.
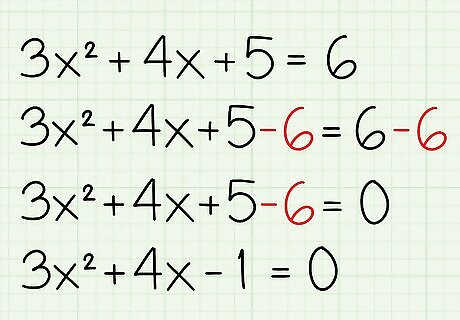
Move the constant terms to the left side of the equation. The constant terms are any terms that aren't attached to a variable. In this case, you have 5 on the left side and 6 on the right side, so subtract 6 from both sides of the equation. Now you have 3 x 2 + 4 x − 1 = 0. {\displaystyle 3x^{2}+4x-1=0.} {\displaystyle 3x^{2}+4x-1=0.}
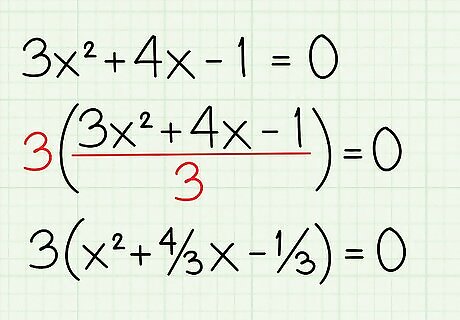
Factor out the coefficient of the squared term. In this case, 3 is the coefficient of the x 2 {\displaystyle x^{2}} x^{{2}} term. Divide each term by 3, then put the terms into parenthesis with a 3 in front. So, . Now the equation is: 3 ( x 2 + 4 3 x − 1 3 ) = 0. {\displaystyle 3(x^{2}+{\frac {4}{3}}x-{\frac {1}{3}})=0.} {\displaystyle 3(x^{2}+{\frac {4}{3}}x-{\frac {1}{3}})=0.}
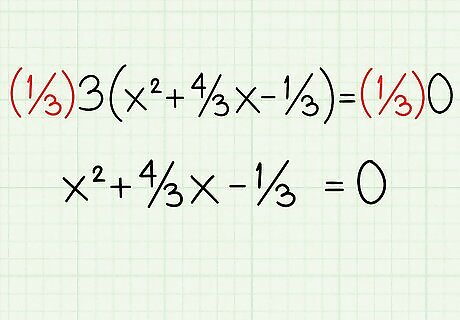
Divide by the constant you just factored out. Since you divided each term by 3, it can be removed without impacting the equation. Now you have x 2 + 4 3 x − 1 3 = 0. {\displaystyle x^{2}+{\frac {4}{3}}x-{\frac {1}{3}}=0.} {\displaystyle x^{2}+{\frac {4}{3}}x-{\frac {1}{3}}=0.}
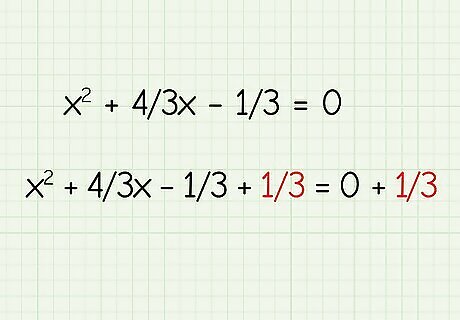
Move the constant to the right side of the equation. Isolate the x terms by moving − 1 3 {\displaystyle -{\frac {1}{3}}} -{\frac {1}{3}} to the other side of the equal sign. x 2 + 4 3 x − 1 3 + 1 3 = 0 + 1 3 {\displaystyle x^{2}+{\frac {4}{3}}x-{\frac {1}{3}}+{\frac {1}{3}}=0+{\frac {1}{3}}} {\displaystyle x^{2}+{\frac {4}{3}}x-{\frac {1}{3}}+{\frac {1}{3}}=0+{\frac {1}{3}}}
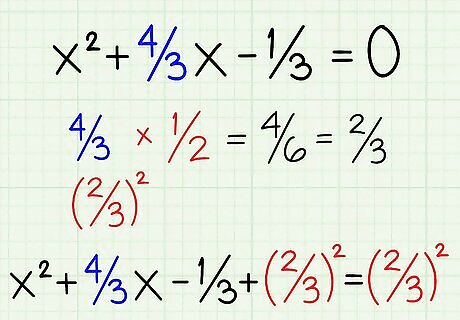
Halve the second term and square it. Next, take the second term, 4 3 {\displaystyle {\frac {4}{3}}} {\frac {4}{3}}, also known as the b term, and halve and square it to complete the square. When you’re done, add it to both sides of the equation to keep it balanced. x 2 + 4 3 x + 4 9 = 1 3 + 4 9 {\displaystyle x^{2}+{\frac {4}{3}}x+{\frac {4}{9}}={\frac {1}{3}}+{\frac {4}{9}}} {\displaystyle x^{2}+{\frac {4}{3}}x+{\frac {4}{9}}={\frac {1}{3}}+{\frac {4}{9}}} 4 3 ∗ 1 2 = 2 3 {\displaystyle {\frac {4}{3}}*{\frac {1}{2}}={\frac {2}{3}}} {\displaystyle {\frac {4}{3}}*{\frac {1}{2}}={\frac {2}{3}}} 2 2 3 2 = 4 9 {\displaystyle {\frac {2^{2}}{3^{2}}}={\frac {4}{9}}} {\displaystyle {\frac {2^{2}}{3^{2}}}={\frac {4}{9}}}
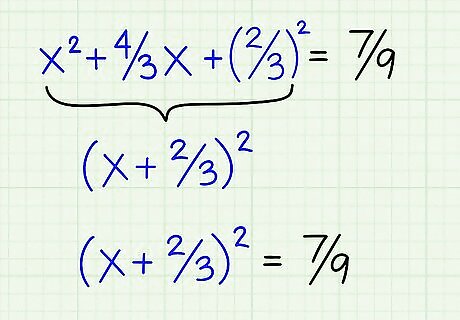
Write the left side of the equation as a perfect square. Since you've already used a formula to find the missing term, all you have to do is put x and half of the second coefficient in parentheses and square them, like so: ( x + 2 3 ) 2 {\displaystyle (x+{\frac {2}{3}})^{2}} {\displaystyle (x+{\frac {2}{3}})^{2}}. The equation should now read: ( x + 2 3 ) 2 = 7 9 {\displaystyle (x+{\frac {2}{3}})^{2}={\frac {7}{9}}} {\displaystyle (x+{\frac {2}{3}})^{2}={\frac {7}{9}}}. Note that factoring that perfect square will give you the three terms: x 2 + 4 3 x + 4 9 {\displaystyle x^{2}+{\frac {4}{3}}x+{\frac {4}{9}}} {\displaystyle x^{2}+{\frac {4}{3}}x+{\frac {4}{9}}}.
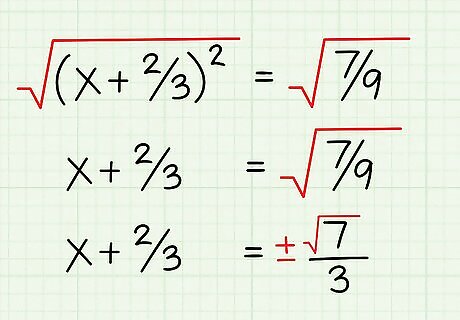
Take the square root of both sides. On the left side of the equation, the square root of ( x + 2 3 ) 2 {\displaystyle (x+{\frac {2}{3}})^{2}} {\displaystyle (x+{\frac {2}{3}})^{2}} is just x + 2 3 {\displaystyle x+{\frac {2}{3}}} {\displaystyle x+{\frac {2}{3}}}. On the right side, the square root of the denominator, 9, is 3, and the square root of 7 is 7 {\displaystyle {\sqrt {7}}} {\sqrt {7}}, so the square root is ± 7 3 {\displaystyle {\frac {\sqrt {7}}{3}}} {\displaystyle {\frac {\sqrt {7}}{3}}}. Remember to write +/- because a square root can be positive or negative.

Isolate the variable. To isolate the variable x, move the constant term 2 3 {\displaystyle {\frac {2}{3}}} {\frac {2}{3}} over to the right side of the equation. You now have two possible answers for x: ± 7 3 − 2 3 {\displaystyle {\frac {\sqrt {7}}{3}}-{\frac {2}{3}}} {\displaystyle {\frac {\sqrt {7}}{3}}-{\frac {2}{3}}}. You can leave it at that or find the actual square root of 7 if you need an answer without the radical sign.




















Comments
0 comment