
views
- To convert a fraction to a decimal, divide the numerator, or the top number in the fraction, by the denominator, which is the bottom number in the fraction.
- To use long division, place your denominator on the outside of the box and your numerator inside the box, then divide.
- For denominators that are factors of 10 (like 100 or 1,000), move the decimal to the left of the numerator as many places as you have zeros in the denominator.
Converting Fractions to Decimals Using Long Division

Put the numerator inside the division box with a decimal and a zero after it. To start the long division problem, draw a division box around your numerator and write the denominator to the left of the box. Place a decimal and a 0 after the numerator. To convert 3 8 {\displaystyle {\frac {3}{8}}} {\frac {3}{8}}: Place the 3 inside the division box and the 8 outside to the left of it. Place a decimal after the 3 and add a 0 to the end to get 3.0. To convert 1 3 {\displaystyle {\frac {1}{3}}} {\frac {1}{3}}: Place the 1 inside the division box and the 3 outside to the left of it. Place a decimal after the 1 and add a 0 to the end to get 1.0. To convert 27 4 {\displaystyle {\frac {27}{4}}} {\displaystyle {\frac {27}{4}}}: Place the 24 inside the division box and the 4 outside to the left of it. 27 4 {\displaystyle {\frac {27}{4}}} {\displaystyle {\frac {27}{4}}} is larger than a whole number, so you don't need to add a decimal or a zero to the numerator.

Ignore the decimal and divide the whole numerator by the denominator. Place a decimal at the top of the box directly over the decimal inside the box. Ignore the decimal inside the box and treat the number inside as a whole number (for example, 1.0 becomes 10). Write how many times you can put the denominator evenly into the numerator at the top of the box and find the remainder inside the box. To convert 3 8 {\displaystyle {\frac {3}{8}}} {\frac {3}{8}}: The 3.0 inside the division box becomes 30. 8 goes into 30 only 3 times, and 8 × 3 = 24 {\displaystyle {8}\times {3}=24} {\displaystyle {8}\times {3}=24}. Place the 3 after the decimal at the top of the box, then 30 − 24 = 6 {\displaystyle {30}-{24}=6} {\displaystyle {30}-{24}=6}, so 6 is left in the box. To convert 1 3 {\displaystyle {\frac {1}{3}}} {\frac {1}{3}}: The 1.0 inside the box becomes 10. 3 goes into 10 only 3 times, and 3 × 3 = 9 {\displaystyle {3}\times {3}=9} {\displaystyle {3}\times {3}=9}. Place a 3 after the decimal at the top of the box, and 10 − 9 = 1 {\displaystyle {10}-{9}=1} {\displaystyle {10}-{9}=1} so 1 is left in the box. To convert 27 4 {\displaystyle {\frac {27}{4}}} {\displaystyle {\frac {27}{4}}}: 4 goes into 27 only 6 times, and 6 × 4 = 24 {\displaystyle {6}\times {4}=24} {\displaystyle {6}\times {4}=24}. Write the 6 before the decimal at the top of the box because 6 is the whole number. Now, we just need to find how much of 27 4 {\displaystyle {\frac {27}{4}}} {\displaystyle {\frac {27}{4}}} is less than 1. At the bottom, write 24 − 27 = 3 {\displaystyle {24}-{27}=3} {\displaystyle {24}-{27}=3}.
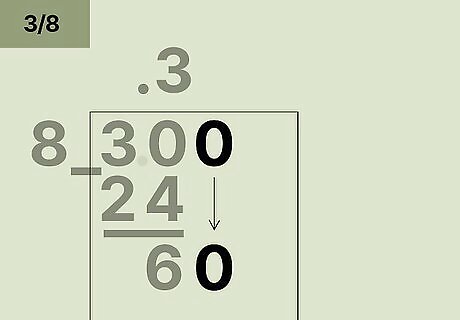
Add another 0 to the end of the number in the box and drag it down to your answer. Place a 0 at the end of your numerator in the box. Draw an arrow from the 0 down to your answer at the bottom and add a 0 to the end of your answer so the number is large enough that you can divide it by the numerator. To convert 3 8 {\displaystyle {\frac {3}{8}}} {\frac {3}{8}}: You can’t divide 6 by 8, so add 0 after 3.0 to get 3.00. Drag the 0 down to your answer at the bottom to get 60, which you can now divide by 8. To convert 1 3 {\displaystyle {\frac {1}{3}}} {\frac {1}{3}}: You can’t divide 1 by 3, so place a 0 after 1.0 inside the box to get 1.00. Draw an arrow from the new 0 down to your answer. Adding a 0 to the end of 1 equals 10, which you can now divide by 3. To convert 27 4 {\displaystyle {\frac {27}{4}}} {\displaystyle {\frac {27}{4}}}: Place a decimal after 27 and add a 0 after it to get 27.0. Draw an arrow from the new 0 to your answer of 3 to get 30, which you can now divide by 4.

Keep dividing until you get 0 or a repeating number. If you still have a remainder after dividing, place a 0 at the end of your numerator and your answer and divide them again. If you keep getting the same number or if you get 0 as your answer, you’re done with the problem. To convert 3 8 {\displaystyle {\frac {3}{8}}} {\frac {3}{8}}: You can put 8 into 60 just 7 times, and 8 × 7 = 56 {\displaystyle {8}\times {7}=56} {\displaystyle {8}\times {7}=56}. Add a 7 to the right of your answer at the top of the box. Then, find the remainder: 60 − 56 = 4 {\displaystyle {60}-{56}=4} {\displaystyle {60}-{56}=4}. Write a 0 after your numerator, then write a 0 after your answer at the bottom to get 40. You can put 8 into 40 evenly 5 times. 8 × 5 = 40 {\displaystyle {8}\times {5}=40} {\displaystyle {8}\times {5}=40} and 40 − 40 = 0 {\displaystyle {40}-{40}=0} {\displaystyle {40}-{40}=0}. Place the 5 to the right of your answer at the top, and you’re done! Final answer: 0.375 To convert 1 3 {\displaystyle {\frac {1}{3}}} {\frac {1}{3}}: You can put 3 into 10 just 3 times, and 3 × 3 = 9 {\displaystyle {3}\times {3}=9} {\displaystyle {3}\times {3}=9}. Add a 3 to the right of your answer at the top and subtract 9 from 10 to get 1. Notice a pattern? If you continue dividing, you’ll keep getting a remainder of 1 and continue to place 3 at the top of the box. Since you keep getting the same number, you’re done with the problem! Final answer: 0.333333 repeating To convert 27 4 {\displaystyle {\frac {27}{4}}} {\displaystyle {\frac {27}{4}}}: 4 goes into 30 just 7 times, and 4 × 7 = 28 {\displaystyle {4}\times {7}=28} {\displaystyle {4}\times {7}=28}. Place the 7 after the decimal at the top of the box. At the bottom, write 30 − 28 = 2 {\displaystyle {30}-{28}=2} {\displaystyle {30}-{28}=2}. Place a 0 after the 27.0 to get 27.00. Draw an arrow down to your answer, then place a 0 after the 2 to get 20. 4 goes into 20 evenly 5 times. 4 t i m e s 5 = 20 {\displaystyle {4}times{5}=20} {\displaystyle {4}times{5}=20} and 20 − 20 = 0 {\displaystyle {20}-{20}=0} {\displaystyle {20}-{20}=0}. Place the 5 at the top of the box. Since the answer is 0, you’re done with the problem! Final answer: 6.75
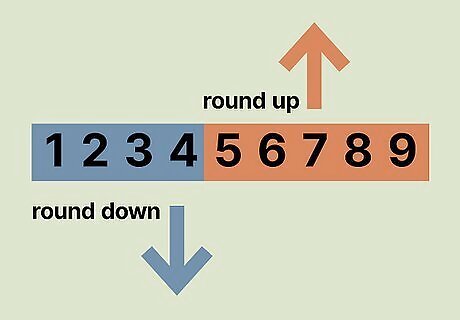
For repeating decimals, round it to the nearest hundredth or thousandth. If you have a number where the last digits repeat over and over, round it to the nearest hundredths or thousandths place. For example, if your answer is 0.375555, you can round it to the thousandth's place to get 0.376, or the hundredth's place to get 0.38. If the number you’re rounding from is a 5 or higher, round up. If your number is 4 or lower, round down. If you don’t need a certain number of place values in your answer, draw a bar over the numbers that repeat to show that they’re going to repeat over and over forever. For example, 0.333 repeating can be also be written 0.33 ¯ {\displaystyle {\overline {0.33}}} {\displaystyle {\overline {0.33}}}.
Converting Fractions to Decimals Using Powers of 10
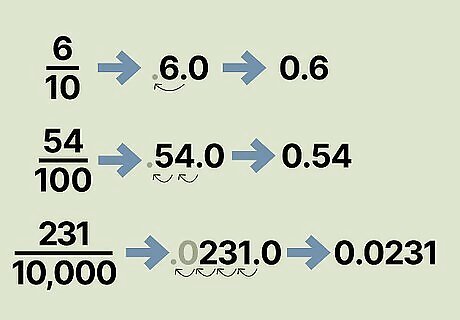
Shift the decimal in the numerator to the left the number of zeroes in the denominator. Numbers with factors of 10 like 10, 100, 1,000, or 10,000 in the denominator can be easily turned into decimals. To get your answer, write down the numerator and move the decimal to the left the same number of spaces as you have zeroes in your denominator. If your fraction is 6 10 {\displaystyle {\frac {6}{10}}} {\displaystyle {\frac {6}{10}}}, write down 6.0 and move the decimal from the right of the number over 1 space to get 0.6 as your answer. If your fraction is 54 100 {\displaystyle {\frac {54}{100}}} {\displaystyle {\frac {54}{100}}}, write down 54.0 and move the decimal 2 spaces to the left to get 0.54 as your answer. If your fraction is 231 10 , 000 {\displaystyle {\frac {231}{10,000}}} {\displaystyle {\frac {231}{10,000}}}, write down 231.0. Since there are 4 zeroes in 10,000, move the decimal after 231 to the left 4 spaces to get 0.0231.
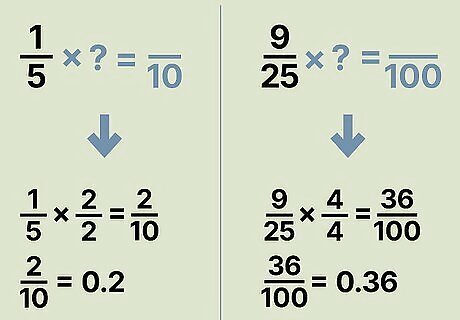
Multiply the numerator by a common factor to get a power 10 denominator. Look for numbers with denominators that can be multiplied by another number to get a factor of 10. Multiply both the numerator and the denominator by that number to get a factor of 10 in the denominator, then move the decimal to the left the same number of spaces as you have zeroes in your denominator. The 5 in 1 5 {\displaystyle {\frac {1}{5}}} {\frac {1}{5}} can be multiplied by 2 to get 10. 1 5 × 2 2 = 2 10 {\displaystyle {\frac {1}{5}}\times {\frac {2}{2}}={\frac {2}{10}}} {\displaystyle {\frac {1}{5}}\times {\frac {2}{2}}={\frac {2}{10}}} Write down 2.0. Because there’s 1 zero in 10, move the decimal to the left 1 place to get 0.2 as your answer. The 25 in 9 25 {\displaystyle {\frac {9}{25}}} {\displaystyle {\frac {9}{25}}} can be multiplied by 4 to get 100. 9 25 × 4 4 = 36 100 {\displaystyle {\frac {9}{25}}\times {\frac {4}{4}}={\frac {36}{100}}} {\displaystyle {\frac {9}{25}}\times {\frac {4}{4}}={\frac {36}{100}}}. Write down 36.0. Since there are 2 zeroes in 100, move the decimal to the left 2 spaces to get 0.36. To make your calculations faster, try writing down basic fraction/decimal equivalents like 1 4 = 0.25 {\displaystyle {\frac {1}{4}}=0.25} {\displaystyle {\frac {1}{4}}=0.25}, 1 2 = 0.5 {\displaystyle {\frac {1}{2}}=0.5} {\displaystyle {\frac {1}{2}}=0.5}, and 3 4 = 0.75 {\displaystyle {\frac {3}{4}}=0.75} {\displaystyle {\frac {3}{4}}=0.75} on flashcards and quiz yourself regularly.
Understanding Fractions and Decimals
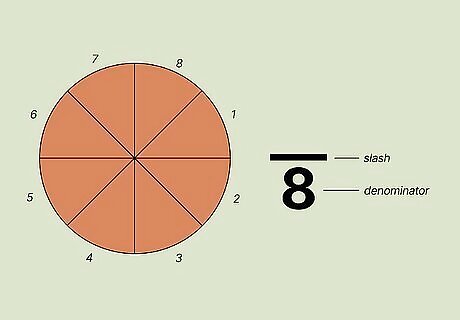
In a fraction, the denominator, or the bottom number, is how many parts are in a whole. Each fraction has a numerator, or the top number, a slash, which goes between the numbers, and a denominator, which is the bottom number in the fraction. The denominator represents how many equal parts there are in the whole, like how many slices are in a whole pepperoni pizza. For example, a pizza might be cut into 8 slices. The denominator for the pizza would then be 8.

In a fraction, the numerator, or the top number, is how many parts there are. While the denominator represents how many parts a whole is split into, the numerator represents how many equal parts are actually there, like how many slices are left in a whole pepperoni pizza after a group of people have eaten part of it. For example, a pizza might only have 1 slice left out of its 8 slices. So, 1 piece of this pizza would be equal to the fraction 1 8 {\displaystyle {\frac {1}{8}}} {\frac {1}{8}}.
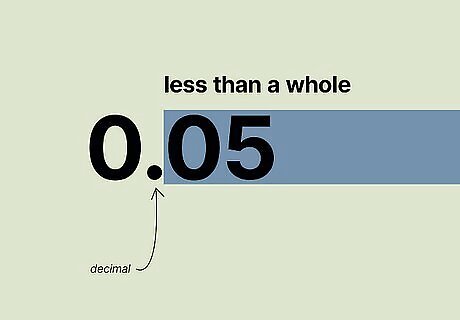
In a decimal, all the numbers to the right of the decimal represent less than a whole. Decimal numbers don’t have a slash to show how much of a whole number is left. Instead, all the numbers to the right of the decimal point represent the numbers that are less than a whole. Decimals are also often read in a way that shows how similar they are to fractions. For example, 0.05 would commonly be read aloud as "five-hundredths," which is the same as 5 100 {\displaystyle {\frac {5}{100}}} {\displaystyle {\frac {5}{100}}}, or “five-hundredths.”

















Comments
0 comment