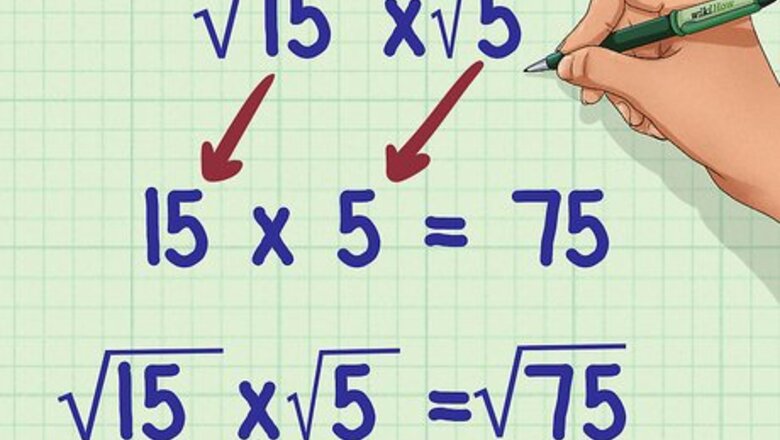
views
Multiplying Square Roots Without Coefficients
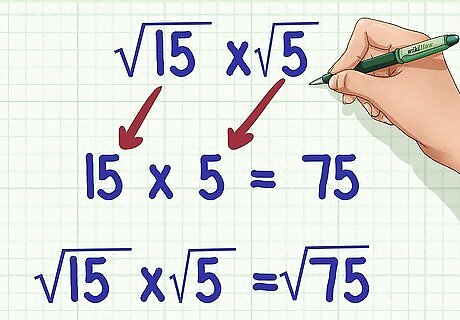
Multiply the radicands. A radicand is a number underneath the radical sign. To multiply radicands, multiply the numbers as if they were whole numbers. Make sure to keep the product under one radical sign. For example, if you are calculating 15 × 5 {\displaystyle {\sqrt {15}}\times {\sqrt {5}}} {\sqrt {15}}\times {\sqrt {5}}, you would calculate 15 × 5 = 75 {\displaystyle 15\times 5=75} 15\times 5=75. So, 15 × 5 = 75 {\displaystyle {\sqrt {15}}\times {\sqrt {5}}={\sqrt {75}}} {\sqrt {15}}\times {\sqrt {5}}={\sqrt {75}}.
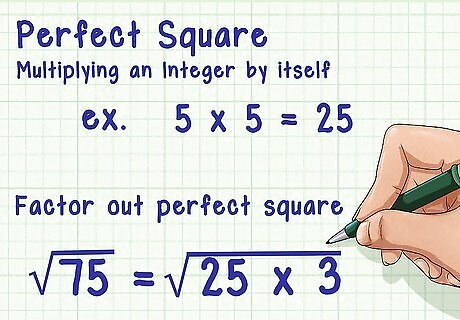
Factor out any perfect squares in the radicand. To do this, see whether any perfect square is a factor of the radicand. If you cannot factor out a perfect square, your answer is already simplified and you need not do anything further. A perfect square is the result of multiplying an integer (a positive or negative whole number) by itself. For example, 25 is a perfect square, because 5 × 5 = 25 {\displaystyle 5\times 5=25} 5\times 5=25. For example, 75 {\displaystyle {\sqrt {75}}} {\sqrt {75}} can be factored to pull out the perfect square 25: 75 {\displaystyle {\sqrt {75}}} {\sqrt {75}}= 25 × 3 {\displaystyle {\sqrt {25\times 3}}} {\sqrt {25\times 3}}
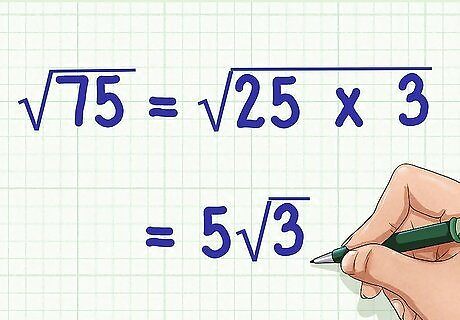
Place the square root of the perfect square in front of the radical sign. Keep the other factor under the radical sign. This will give you your simplified expression. For example, 75 {\displaystyle {\sqrt {75}}} {\sqrt {75}} can be factored as 25 × 3 {\displaystyle {\sqrt {25\times 3}}} {\sqrt {25\times 3}}, so you would pull out the square root of 25 (which is 5): 75 {\displaystyle {\sqrt {75}}} {\sqrt {75}}= 25 × 3 {\displaystyle {\sqrt {25\times 3}}} {\sqrt {25\times 3}}= 5 3 {\displaystyle 5{\sqrt {3}}} 5{\sqrt {3}}
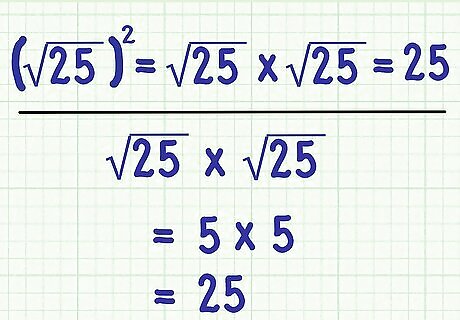
Square a square root. In some instances, you will need to multiply a square root by itself. Squaring a number and taking the square root of a number are opposite operations; thus, they undo each other. The result of squaring a square root, then, is simply the number under the radical sign. For example, 25 × 25 = 25 {\displaystyle {\sqrt {25}}\times {\sqrt {25}}=25} {\sqrt {25}}\times {\sqrt {25}}=25. You get that result because 25 × 25 = 5 × 5 = 25 {\displaystyle {\sqrt {25}}\times {\sqrt {25}}=5\times 5=25} {\sqrt {25}}\times {\sqrt {25}}=5\times 5=25.
Multiplying Square Roots With Coefficients
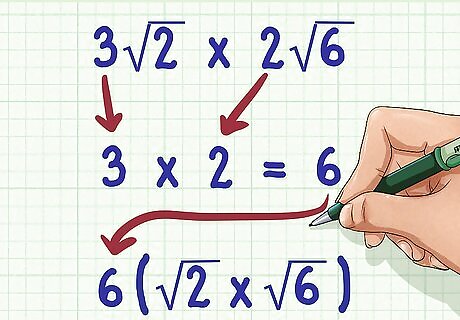
Multiply the coefficients. A coefficient is a number in front of the radical sign. To do this, just ignore the radical sign and radicand, and multiply the two whole numbers. Place their product in front of the first radical sign. Pay attention to positive and negative signs when multiplying coefficients. Don't forget that a negative times a positive is a negative, and a negative times a negative is a positive. For example, if you are calculating 3 2 × 2 6 {\displaystyle 3{\sqrt {2}}\times 2{\sqrt {6}}} 3{\sqrt {2}}\times 2{\sqrt {6}}, you would first calculate 3 × 2 = 6 {\displaystyle 3\times 2=6} 3\times 2=6. So now your problem is 6 2 × 6 {\displaystyle 6{\sqrt {2}}\times {\sqrt {6}}} 6{\sqrt {2}}\times {\sqrt {6}}.
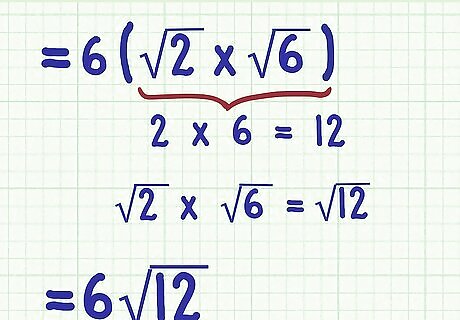
Multiply the radicands. To do this, multiply the numbers as if they were whole numbers. Make sure to keep the product under the radical sign. For example, if the problem is now 6 2 × 6 {\displaystyle 6{\sqrt {2}}\times {\sqrt {6}}} 6{\sqrt {2}}\times {\sqrt {6}}, to find the product of the radicands, you would calculate 2 × 6 = 12 {\displaystyle 2\times 6=12} 2\times 6=12, so 2 × 6 = 12 {\displaystyle {\sqrt {2}}\times {\sqrt {6}}={\sqrt {12}}} {\sqrt {2}}\times {\sqrt {6}}={\sqrt {12}}. The problem now becomes 6 12 {\displaystyle 6{\sqrt {12}}} 6{\sqrt {12}}.
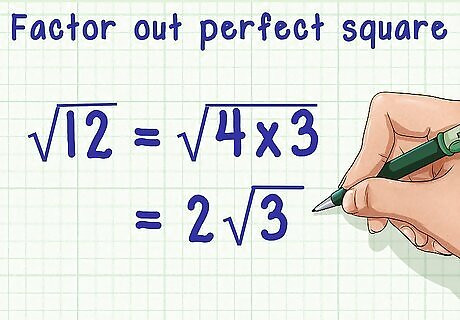
Factor out any perfect squares in the radicand, if possible. You need to do this to simplify your answer. If you cannot pull out a perfect square, your answer is already simplified and you can skip this step. A perfect square is the result of multiplying an integer (a positive or negative whole number) by itself. For example, 4 is a perfect square, because 2 × 2 = 4 {\displaystyle 2\times 2=4} 2\times 2=4. For example, 12 {\displaystyle {\sqrt {12}}} {\sqrt {12}} can be factored to pull out the perfect square 4: 12 {\displaystyle {\sqrt {12}}} {\sqrt {12}}= 4 × 3 {\displaystyle {\sqrt {4\times 3}}} {\sqrt {4\times 3}}
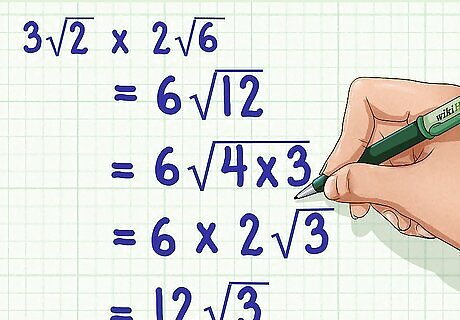
Multiply the square root of the perfect square by the coefficient. Keep the other factor under the radicand. This will give you your simplified expression. For example, 6 12 {\displaystyle 6{\sqrt {12}}} 6{\sqrt {12}} can be factored as 6 4 × 3 {\displaystyle 6{\sqrt {4\times 3}}} 6{\sqrt {4\times 3}}, so you would pull out the square root of 4 (which is 2) and multiply it by 6: 6 12 {\displaystyle 6{\sqrt {12}}} 6{\sqrt {12}}= 6 4 × 3 {\displaystyle 6{\sqrt {4\times 3}}} 6{\sqrt {4\times 3}}= 6 × 2 3 {\displaystyle 6\times 2{\sqrt {3}}} 6\times 2{\sqrt {3}}= 12 3 {\displaystyle 12{\sqrt {3}}} 12{\sqrt {3}}

















Comments
0 comment