How to Find the Magnitude of a Vector

Bionous

Editor

posted on 11 years ago — updated on 1 second ago

54
views

A vector is a geometrical object that has both a magnitude and direction.[1]
X
Research source

The magnitude is the length of the vector, while the direction is the way it's pointing. Calculating the magnitude of a vector is simple with a few easy steps. Other important vector operations include adding and subtracting vectors, finding the angle between two vectors, and finding the cross product.

Steps

Finding the Magnitude of a Vector at the Origin

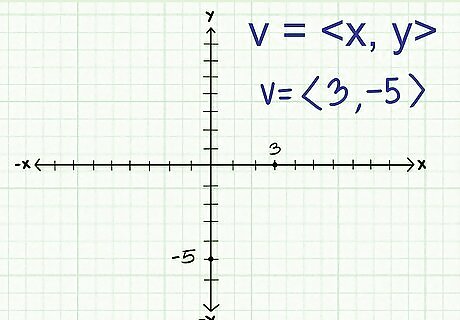
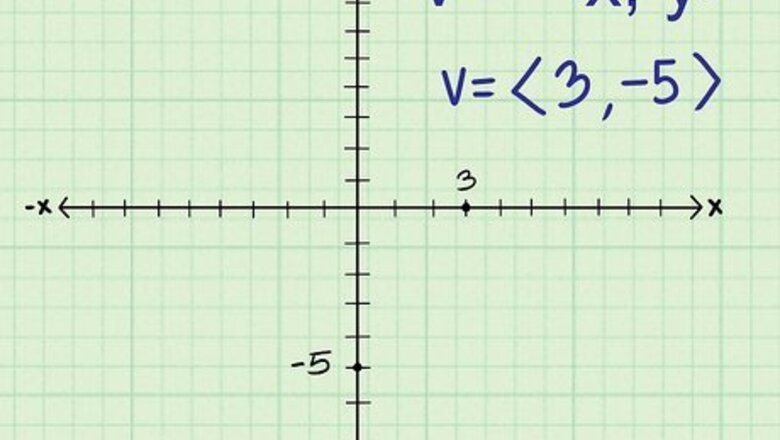
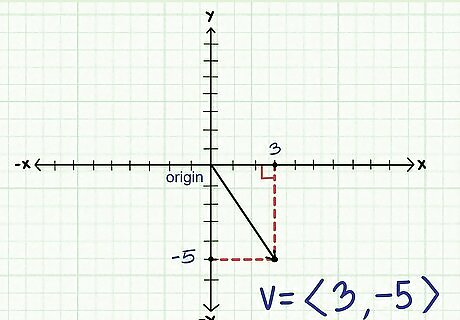
Determine the components of the vector. Every vector can be numerically represented in the Cartesian coordinate system with a horizontal (x-axis) and vertical (y-axis) component. It is written as an ordered pair v =< x , y > {\displaystyle v=} v=. For example, the vector above has a horizontal component of 3 and a vertical component of -5, therefore the ordered pair is <3, -5>.

Draw a vector triangle. When you draw the horizontal and vertical components, you end up with a right triangle. The magnitude of the vector is equal to the hypotenuse of the triangle so you can use the Pythagorean theorem to calculate it.

Rearrange the Pythagorean theorem to calculate the magnitude. The Pythagorean theorem is A + B = C. “A” and “B” are the horizontal and vertical components of the triangle while “C” is the hypotenuse. Since the vector is the hypotenuse you want to solve for “C”. x + y = v v = √(x + y))

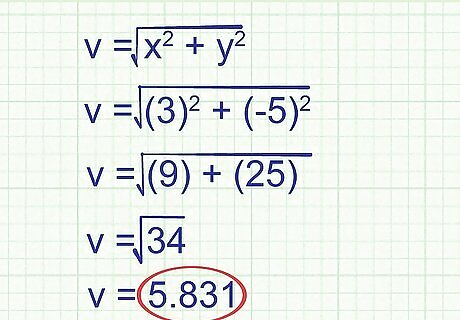
Solve for the magnitude. Using the equation above, you can plug in the numbers of the ordered pair of the vector to solve for the magnitude. For example, v = √((3+(-5))) v =√(9 + 25) = √34 = 5.831 Don't worry if your answer is not a whole number. Vector magnitudes can be decimals.

Finding the Magnitude of a Vector Away from the Origin

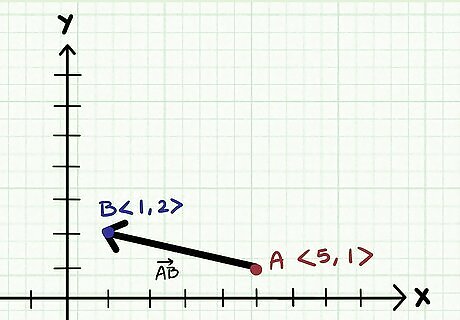
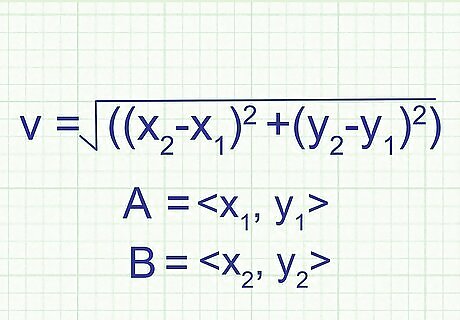
Determine the components of both points of the vector. Every vector can be numerically represented in the Cartesian coordinate system with a horizontal (x-axis) and vertical (y-axis) component. It is written as an ordered pair v =< x , y > {\displaystyle v=} v=. If you are given a vector that is placed away from the origin of the Cartesian coordinate system, you must define the components of both points of the vector. For example, the vector AB has an ordered pair for point A and point B. Point A has a horizontal component of 5 and a vertical component of 1, so the ordered pair is <5, 1>. Point B has a horizontal component of 1 and a vertical component of 2, so the ordered pair is <1, 2>.

Use a modified formula to solve for the magnitude. Because you now have two points you are dealing with, you must subtract the x and y components of each point before you solve using the equation v = √((x2-x1) +(y2-y1)). Point A is ordered pair 1 and point B is ordered pair 2

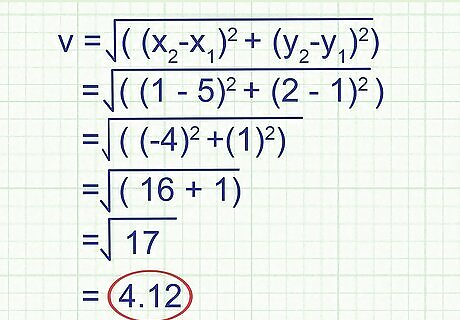
Solve for the magnitude. Plug in the numbers of your ordered pairs and calculate the magnitude. Using our above example the calculation looks like this: v = √((x2-x1) +(y2-y1)) v = √((1-5) +(2-1)) v = √((-4) +(1)) v = √(16+1) = √(17) = 4.12 Don't worry if your answer is not a whole number. Vector magnitudes can be decimals.