Lengthy expressions really aren't that hard if you just do things one at a time and in the right order. The reason this exists is so mathematicians have a universal order. Otherwise you could have two different answers to a simple math problem like 2 x 3 + 4.The order of operations gives us instructions on how to simplify expressions that contain more than one operation.
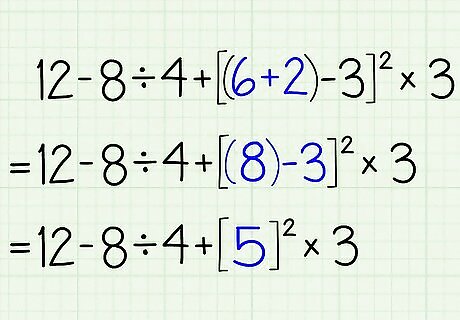
Perform any calculations inside the innermost parenthesis (or any other types of grouping symbols) first. Then progress outward. 12 - 8 ÷ 4 + [(6 + 2) - 3]•312 - 8 ÷ 4 + [(8) - 3]•312 - 8 ÷ 4 + [5]•3
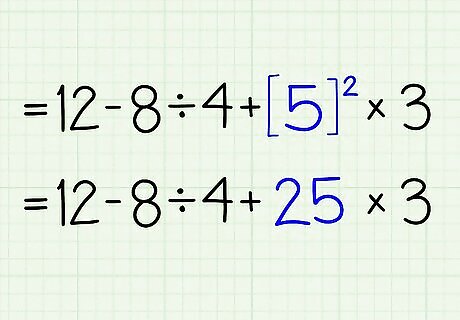
Perform any exponents (roots count too). 12 - 8 ÷ 4 + [5]•312 - 8 ÷ 4 + 25•3
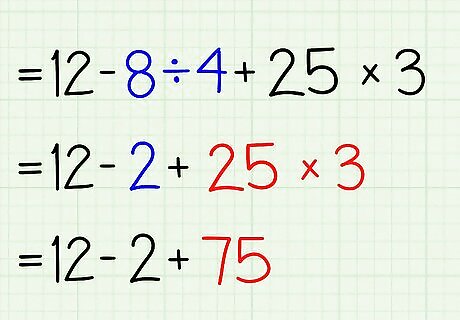
Perform any multiplications or divisions, going from left to right. 12 - 8 ÷ 4 + 25•312 - 2 + 75
Perform any additions or subtractions, going from left to right. 12 - 2 + 7510 + 7585
Comments
0 comment